BIP47, или гадкий утенок

Из этой статьи вы узнаете о принципе работы протоколов BIP47 и PayNym, механизмах работы этих протоколов и практических приложениях, которые из них вытекают.

Перевод статьи Лоика Мореля
Поддержать проект

— Он больно велик! — говорили все, а индейский петух, который родился со шпорами на ногах и потому воображал себя императором, надулся и, словно корабль на всех парусах, подлетел к утенку, поглядел на него и пресердито залопотал; гребешок у него так весь и налился кровью. Бедный утенок просто не знал, что ему делать, как быть. И надо же ему было уродиться таким безобразным, каким-то посмешищем для всего птичьего двора!

Одним из наиболее серьезных бедствий протокола Биткоин является повторное использование адресов. Прозрачность и распределенность сети делает эту практику опасной для конфиденциальности пользователей. Чтобы избежать связанных с этим проблем, рекомендуется использовать новый пустой адрес получения для каждого нового платежа, поступающего на кошелек, что в некоторых случаях может быть затруднительно.

Этот недостаток так же стар, как и “Белая книга”. Сатоши уже предостерегал нас от этого риска в своей книге, опубликованной в конце 2008 года:

В качестве дополнительной защиты следует использовать новую пару ключей для каждой транзакции, чтобы они не были связаны с общим владельцем.

Существует множество решений, позволяющих получать многократные платежи, не прибегая при этом к повторному использованию адреса. Каждое из них имеет свои компромиссы и недостатки. Среди всех этих решений можно выделить BIP47 - предложение для генерации многократно используемых платежных кодов, разработанное Юстусом Ранвье и опубликованное в 2015 году. Их цель - обеспечить возможность проведения нескольких транзакций в пользу одного и того же лица без повторного использования адреса.

Первоначально это предложение было встречено частью сообщества пренебрежительно и так и не было добавлено в Bitcoin Core. Однако некоторые разработчики все же решили реализовать его. Так, кошелек Samourai Wallet разработал собственную реализацию BIP47: PayNym. Сегодня эта реализация доступна не только в Samourai Wallet для смартфонов, но и в Sparrow Wallet для ПК.

Со временем Samourai разработал новые функции, непосредственно связанные с PayNym. Теперь на базе PayNym и BIP47 существует целая экосистема инструментов для оптимизации конфиденциальности пользователей.

Из этой статьи вы узнаете о принципе работы протоколов BIP47 и PayNym, механизмах работы этих протоколов и практических приложениях, которые из них вытекают. Я расскажу только о первой версии BIP47, той, которая сейчас используется для PayNym, но версии 2, 3 и 4 работают практически идентично.

Единственное существенное отличие заключается в транзакции уведомления. В версии 1 для уведомления используется простой адрес с OP_RETURN, в версии 2 - multisig скрипт (bloom-multisig) с OP_RETURN, а в версиях 3 и 4 - просто multisig скрипт (cfilter-multisig). Таким образом, упомянутые в данной статье механизмы и, в частности, рассмотренные криптографические методы, применимы ко всем четырем версиям. На сегодняшний день в реализации PayNym в кошельках Samourai и Sparrow используется первая версия BIP47.

Проблема повторного использования адресов #

Адрес приема используется для получения биткоинов. Он генерируется на основе публичного ключа путем его хеширования и применения к нему определенного формата. Он может быть использован для создания нового условия расходования монеты с целью смены ее владельца.

Более того, вы наверняка уже слышали от осведомленного биткоинера, что адреса приема предназначены для одноразового использования, то есть для каждого нового платежа, поступающего в ваш портфель, необходимо генерировать новый. Хорошо, но зачем?

В принципе, повторное использование адресов не несет прямой угрозы вашим средствам. Использование криптографии на эллиптических кривых позволяет доказать сети, что вы владеете приватным ключом, не раскрывая сам ключ. Таким образом, вы можете заблокировать несколько разных UTXO на одном и том же адресе и потратить их в разное время. Если вы не раскроете приватный ключ, связанный с этим адресом, никто не сможет получить доступ к вашим средствам. Проблема повторного использования адресов - это скорее проблема конфиденциальности.

Как уже говорилось во введении, прозрачность и распределенность сети Биткоин означает, что любой пользователь, при условии наличия у него доступа к Биткоин-узлу, может наблюдать за транзакциями платежной системы. В результате он может видеть балансы различных адресов. Сатоши Накамото упомянул о возможности генерировать новые пары ключей, а значит, и новые адреса, для каждого нового платежа, поступающего в кошелек. Цель заключается в том, чтобы иметь дополнительный барьер на случай выявления связи между личностью пользователя и одной из его пар ключей.

Сегодня, с появлением компаний, занимающихся анализом блокчейна, и развитием KYC, использование пустых адресов - это уже не дополнительный барьер, а обязанность каждого, кто хоть немного заботится о своей конфиденциальности.

Стремление к приватности - это не излишняя забота или фантазия максималиста-биткоинера. Это конкретный параметр, напрямую влияющий на вашу личную безопасность и сохранность ваших средств. Чтобы вам было понятнее, приведем вполне конкретный пример:

Боб покупает биткоин по системе DCA (Dollars Cost Average), то есть приобретает небольшое количество биткоинов через регулярные промежутки времени, чтобы сгладить цену входа. Боб систематически отправляет приобретенные средства на один и тот же адрес получения. Каждую неделю он покупает 0.01 биткоина и отправляет их на тот же адрес. Через два года Боб накопил на этом адресе целый биткоин.
Булочная за углом принимает оплату в биткоинах. Довольный Боб идет покупать свою булочку за сатоши. Для оплаты он использует заблокированные средства со своего адреса. Теперь его пекарь знает, что он владеет биткоинами. Такая крупная сумма может вызвать зависть у окружающих, а Боб потенциально может подвергнуться физическому нападению.

Таким образом, повторное использование адресов позволяет наблюдателю установить неоспоримую связь между различными UTXO, а значит, иногда и между вашей личностью и всем портфелем.

Именно по этой причине большинство биткоин-кошельков автоматически генерируют новый адрес приема при нажатии на кнопку “Получить”. Поэтому для обычного пользователя необходимость использовать пустые адреса не является большим недостатком. С другой стороны, для онлайн-бизнеса, биржи или кампании по сбору пожертвований это ограничение может быстро стать невыполнимым.

Существует множество решений для таких организаций. Каждое из них имеет свои достоинства и недостатки, но на сегодняшний день, как мы увидим далее, BIP47 действительно отличается от других.

Проблема повторного использования адресов в Биткоине далеко не так незначительна. Как видно из приведенного ниже графика, взятого с сайта oxt.me, общий уровень повторного использования адресов Биткоин-пользователями в настоящее время составляет 52%:

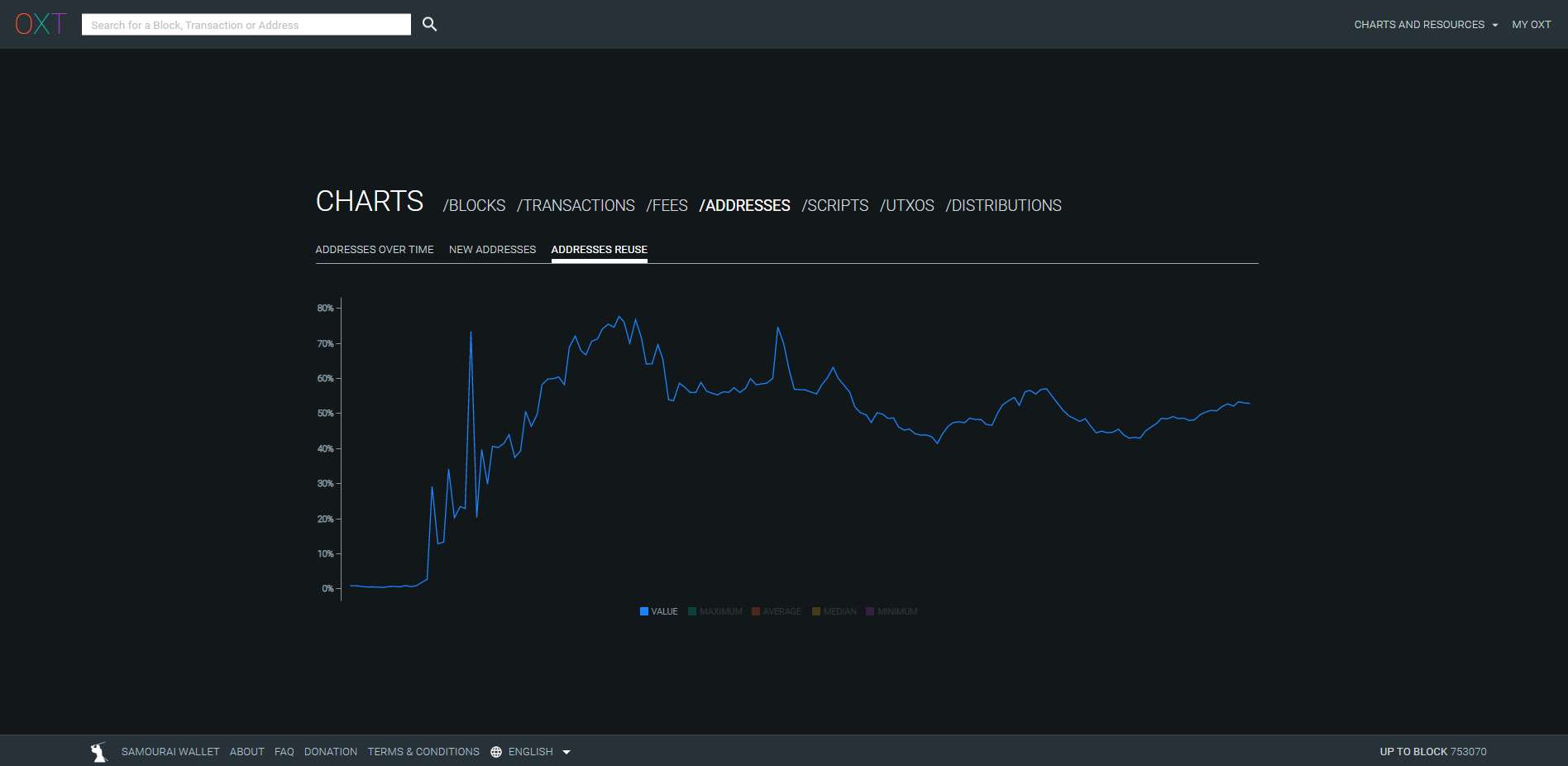
Источник: https://oxt.me/charts

В основном такое повторное использование происходит на биржах, которые из соображений эффективности и удобства многократно используют один и тот же адрес. На сегодняшний день BIP47 является лучшим решением для борьбы с этим явлением на биржах. Это позволило бы снизить общий уровень повторного использования адресов, не создавая при этом особых трудностей для этих организаций.

Этот общий показатель для всей сети в данном случае является особенно уместным. Повторное использование адресов является проблемой не только для того, кто занимается подобной практикой, но и для всех, кто проводит с ним транзакции. Потеря приватности в Биткоине ведет себя как вирус и распространяется от пользователя к пользователю. Если посмотреть на глобальный показатель всех транзакций в сети, то можно получить представление о масштабах этого явления.

Принципы работы BIP47 и PayNym #

Цель BIP47 - предложить простой способ получения большого количества платежей, не прибегая к повторному использованию адресов. Его работа основана на использовании многоразового платежного кода.

Таким образом, несколько отправителей смогут совершить несколько платежей на один многократно используемый платежный код другого пользователя, при этом получателю не придется передавать новый пустой адрес для каждой новой транзакции.

Пользователь может свободно публиковать свой платежный код (в социальных сетях, на своем сайте…) без риска потери конфиденциальности, что не характерно для классического адреса приема или публичного ключа.

Для осуществления платежа оба пользователя должны иметь биткоин-кошелек с реализацией BIP47, например PayNym в Samourai Wallet или Sparrow Wallet. Объединение платежных кодов двух пользователей позволит установить между ними секретный канал. Чтобы правильно установить этот канал, отправитель должен будет провести транзакцию уведомления (подробнее об этом я расскажу позже).

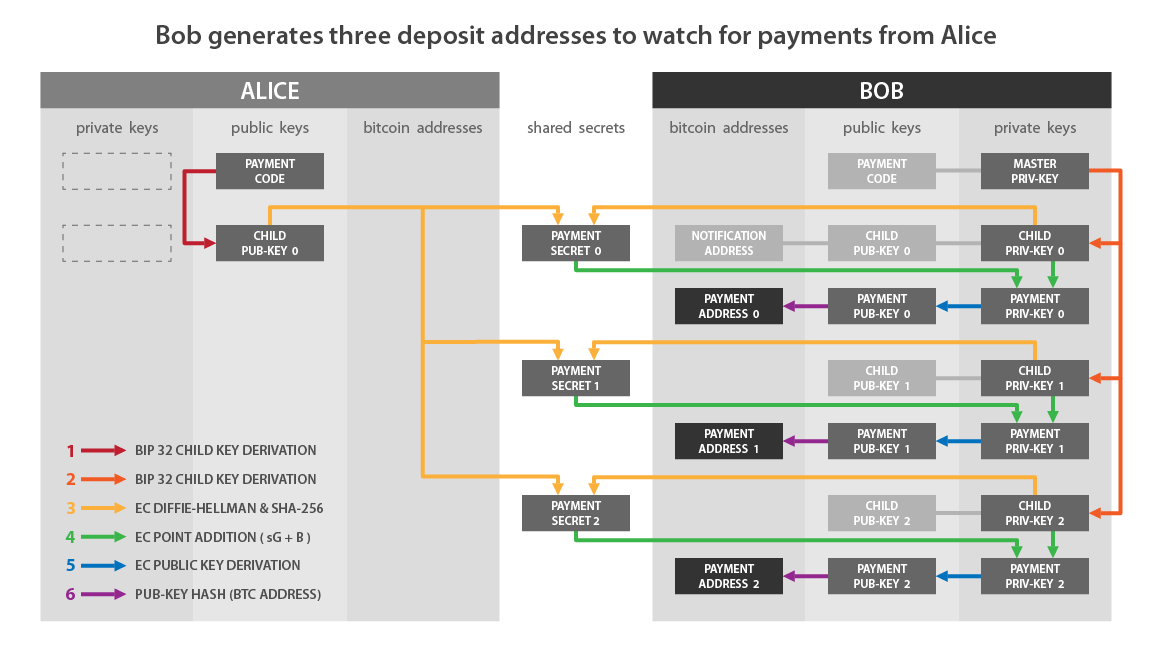
Объединение платежных кодов двух пользователей порождает общие секреты, позволяющие генерировать большое количество уникальных адресов получения биткоина (ровно 2^32). Таким образом, в реальности платеж с помощью BIP47 отправляется не на платежный код, а на вполне классические адреса, которые сами являются производными от платежных кодов участников.

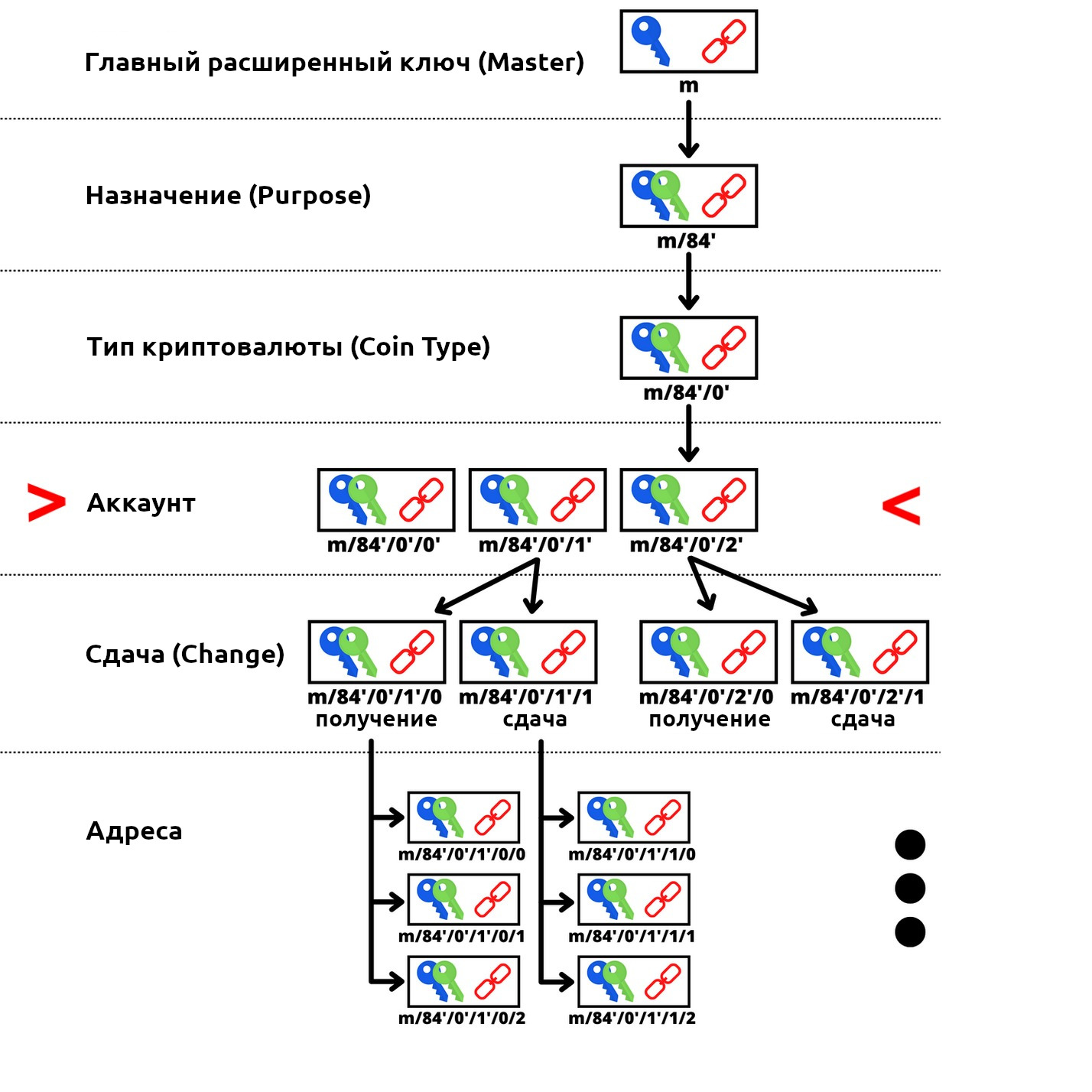
Таким образом, платежный код выступает в роли виртуального идентификатора, полученного из сида кошелька. В структуре путей деривации HD-кошелька платежный код находится на глубине 3, на уровне account.

Путь деривации для BIP47 на уровне purpose имеет индекс 47’ (0x8000002F). Например, путь деривации для многоразового платежного кода будет таким:

m/47'/0'/0'/

Чтобы вы могли представить себе, как выглядит платежный код, вот мой:

PM8TJSBiQmNQDwTogMAbyqJe2PE2kQXjtgh88MRTxsrnHC8zpEtJ8j7Aj628oUFk8X6P5rJ7P5qDudE4Hwq9JXSRzGcZJbdJAjM9oVQ1UKU5j2nr7VR5

Он также может быть закодирован в виде QR-кода для облегчения коммуникации:

Что касается PayNym Bots, этих роботов, которых можно увидеть в Twitter, то они являются просто визуальным отображением вашего платежного кода, созданного Samourai Wallet. Они создаются с помощью хеш-функции, что делает их уникальными. Вот мой с его идентификатором:

+throbbingpond8B1

Эти боты не имеют реального технического применения. Зато они облегчают взаимодействие между пользователями, создавая виртуальный визуальный образ.

Для пользователя процесс осуществления платежа по BIP47 с помощью реализации PayNym предельно прост. Допустим, Алиса хочет отправлять платежи Бобу:

Боб публикует свой QR-код или непосредственно многоразовый платежный код. Их можно разместить на своем сайте, в различных социальных сетях или отправить Алисе с помощью другого средства связи.
Алиса открывает кошелек Samourai или Sparrow и сканирует или вставляет платежный код Боба.
Алиса соединяет свой PayNym с PayNym Боба (“Follow”). Эта операция выполняется вне блокчейна и совершенно бесплатна.
Алиса подключает свой PayNym к PayNym Боба (“Connect”). Эта операция выполняется в блокчейне. Алиса должна заплатить комиссию майнерам, а также фиксированную плату в размере 15000 сатоши за услугу в кошельке Samourai. Плата за услугу взимается также и в Sparrow. Этот этап называется транзакцией уведомления.
После подтверждения транзакции уведомления Алиса может создать транзакцию BIP47 на адрес Боба. Ее кошелек автоматически сгенерирует новый пустой адрес получения, приватный ключ для которого есть только у Боба.

Проведение операции уведомления, т.е. подключение PayNym, является обязательным предварительным шагом для осуществления платежей BIP47. С другой стороны, после его выполнения отправитель сможет совершить множество платежей получателю (ровно 2^32), без необходимости повторного проведения транзакции уведомления.

Как вы уже заметили, существуют две различные операции, позволяющие связать два PayNym: follow и connect. Операция подключения (“connect”) соответствует транзакции уведомления BIP47, которая представляет собой биткоин-транзакцию с определенной информацией, передаваемой в выходе OP_RETURN. Таким образом, с ее помощью устанавливается зашифрованная связь между двумя пользователями для создания общих секретов, необходимых для генерации новых пустых адресов приема.

С другой стороны, операция соединения (“follow” или “link”) позволяет установить связь по протоколу Soroban - это шифрованный протокол связи на базе Tor, специально разработанный командой Samourai Wallet.

Подведем итоги:

Соединение двух PayNym (“follow”) совершенно бесплатно. Это позволяет установить зашифрованную связь вне блокчейна, в частности, для использования инструментов совместных транзакций Samourai (Stowaway или StonewallX2). Эта операция специфична для PayNym. Она не описана в BIP47.
Подключение PayNym является платным. Для этого необходимо выполнить транзакцию уведомления, чтобы инициировать подключение. Ее стоимость складывается из комиссии кошелька, комиссии майнерам и 546 сатоши, отправленных на адрес уведомления получателя, чтобы сообщить ему об открытии канала. Эта операция связана с BIP47. После этого отправитель может произвести множество BIP47-платежей получателю.

Чтобы два кошелька могли взаимодействовать с помощью PayNym, каждый из них должен быть соединен с другим.

Руководство: использование PayNym #

Теперь, когда мы рассмотрели теорию, давайте вместе изучим практику. Идея приведенных ниже уроков заключается в том, чтобы связать мой PayNym в кошельке Sparrow с моим PayNym в кошельке Samourai. В первом уроке показано, как провести транзакцию с использованием многоразового платежного кода из Samourai в Sparrow, а во втором уроке описан тот же механизм из Sparrow в Samourai.

Я сделал эти уроки в Testnet. Это не настоящие биткоины.

Создание транзакции BIP47 с помощью Samourai Wallet #

Для начала вам, очевидно, понадобится приложение Samourai Wallet. Загрузить его можно непосредственно из Google Play Store или скачать APK-файл, доступный на официальном сайте Samourai.

После инициализации кошелька, если вы еще не сделали этого, запросите свой PayNym, нажав на плюс (+) в правом нижнем углу, а затем на “PayNym”.

Первым шагом к осуществлению платежа BIP47 будет получение многоразового платежного кода нашего получателя. Затем мы сможем соединиться с ним (”Follow”) и выполнить подключение (”Connect”):

После подтверждения транзакции уведомления я могу отправлять платежи своему получателю. Каждая транзакция будет проводиться автоматически с новым пустым адресом, ключи от которого есть у получателя. Последнему не нужно выполнять никаких действий, все рассчитывается на моей стороне.

Вот как совершить транзакцию BIP47 в Samorai Wallet:

Создание транзакции BIP47 с помощью Sparrow Wallet #

Как и в случае с Samourai, вам, очевидно, потребуется программное обеспечение Sparrow. Оно доступно для ПК. Скачать его можно с их официального сайта.

Не забудьте проверить подпись разработчика и целостность загруженного программного обеспечения, прежде чем устанавливать его на свой компьютер.

Создайте кошелек и запросите свой PayNym, нажав на кнопку “Show PayNym” в меню “Tools” на верхней панели:

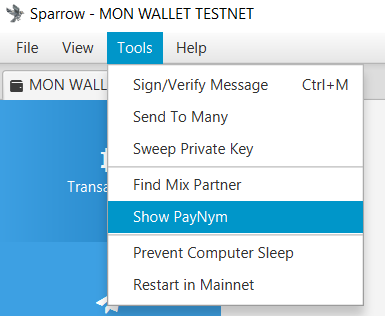
Далее необходимо соединить и подключить свой PayNym к PayNym получателя. Для этого в окне “Find Contact” введите многоразовый платежный код получателя, нажмите “Add Contact”, а затем совершите транзакцию уведомления, нажав на кнопку “Link Contact”:

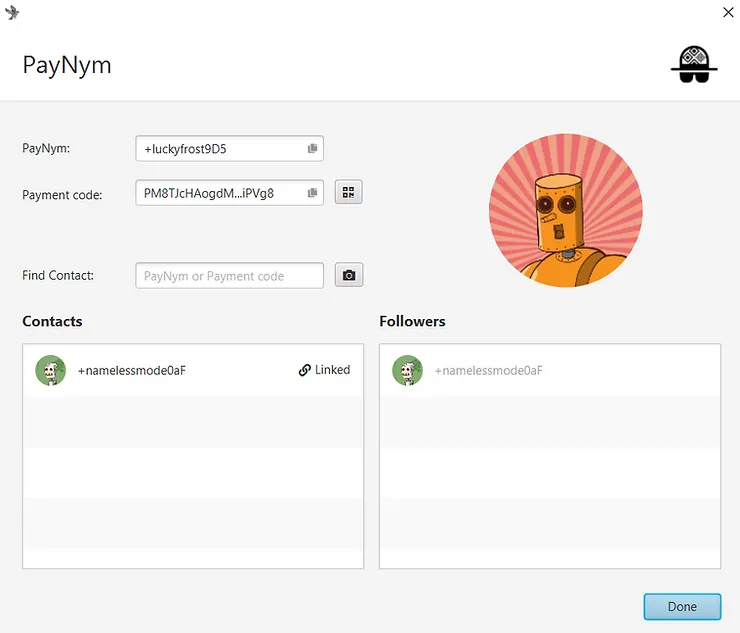
После подтверждения транзакции уведомления можно отправлять платежи на многоразовый платежный код. Вот как это сделать:

Теперь, когда мы смогли изучить практические аспекты реализации BIP47 в PayNym, давайте рассмотрим, как работают все эти механизмы и какие криптографические методы при этом используются.

Как работает BIP47 #

Для изучения механизмов работы BIP47 необходимо понимать структуру иерархического детерминированного кошелька (HD), механизмы получения дочерних пар ключей, а также принципы криптографии на эллиптических кривых.

Многоразовый платежный код #

Как объясняется во второй части данной работы, многоразовый платежный код располагается на глубине 3 в HD-кошельке. В итоге его можно сравнить с xpub, как по размещению и структуре, так и по его роли.

Части, составляющие 80-байтовый платежный код:

Байт 0: Версия. Если мы используем первую версию BIP47, то этот байт будет равен 0x01.
Байт 1: Битовое поле. Это место зарезервировано для указания дополнительных признаков в случае специфического использования. При простом использовании PayNym этот байт будет равен 0x00.
Байт 2: Четность y. Этот байт принимает значение 0x02 или 0x03 в зависимости от четности (четное число или нечетное) значения ординаты нашего публичного ключа.
С 3 байта по 34: Значение x. Эти байты указывают на абсциссу нашего публичного ключа. Конкатенация x и четности y дает наш сжатый публичный ключ.
С 35 байта по 66: Код цепочки (chain code). Это место отведено под код цепочки, связанный с вышеупомянутым публичным ключом.
С 67 байта по 79: Это пространство зарезервировано для возможных будущих разработок. В версии 1 мы просто ставим нули, чтобы заполнить 80 байт - размер данных в выводе OP_RETURN.

Вот шестнадцатеричное представление моего многоразового платежного кода, показанного в предыдущем разделе, с цветами, соответствующими представленным выше байтам:

0x010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000

Далее необходимо добавить байт префикса “P”, чтобы с первого взгляда определить, что вы имеете дело с платежным кодом. Этот байт имеет значение 0x47.

0x47010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000

Наконец, мы вычисляем контрольную сумму этого платежного кода с помощью двойного хеширования с использованием функции SHA256. Мы берем первые четыре байта этого хеша и конкатенируем их в конце (выделены розовым цветом).

0x47010002a0716529bae6b36c5c9aa518a52f9c828b46ad8d907747f0d09dcd4d9a39e97c3c5f37c470c390d842f364086362f6122f412e2b0c7e7fc6e32287e364a7a36a00000000000000000000000000567080c4

Платежный код готов, осталось только преобразовать его в Base 58:

PM8TJSBiQmNQDwTogMAbyqJe2PE2kQXjtgh88MRTxsrnHC8zpEtJ8j7Aj628oUFk8X6P5rJ7P5qDudE4Hwq9JXSRzGcZJbdJAjM9oVQ1UKU5j2nr7VR5

Как видно, эта конструкция очень напоминает структуру расширенного публичного ключа “xpub”.

В процессе получения платежного кода мы использовали сжатый публичный ключ и код цепочки. Эти два элемента являются результатом детерминированной и иерархической деривации из сида кошелька по следующему пути: m/47’/0’/0’/.

Для получения публичного ключа и кода цепочки многоразового платежного кода мы вычисляем главный приватный ключ из сида, затем получаем дочернюю пару с индексом 47 + 2^31 (усиленная деривация). Затем получаем две дочерние пары с индексом 2^31 (усиленная деривация).

Криптографический протокол: обмен ключами Диффи-Хеллмана на эллиптических кривых (ECDH) #

Криптографический протокол, используемый в BIP47 называется ECDH (Elliptic-Curve Diffie-Hellman). Этот протокол является вариантом классического обмена ключами Диффи-Хеллмана.

Диффи-Хеллман в своей первой версии - это протокол обмена ключами, представленный в 1976 году, который позволяет двум людям, используя две пары (публичный и приватный) ключей, установить общий секрет путем обмена по незащищенному каналу связи.

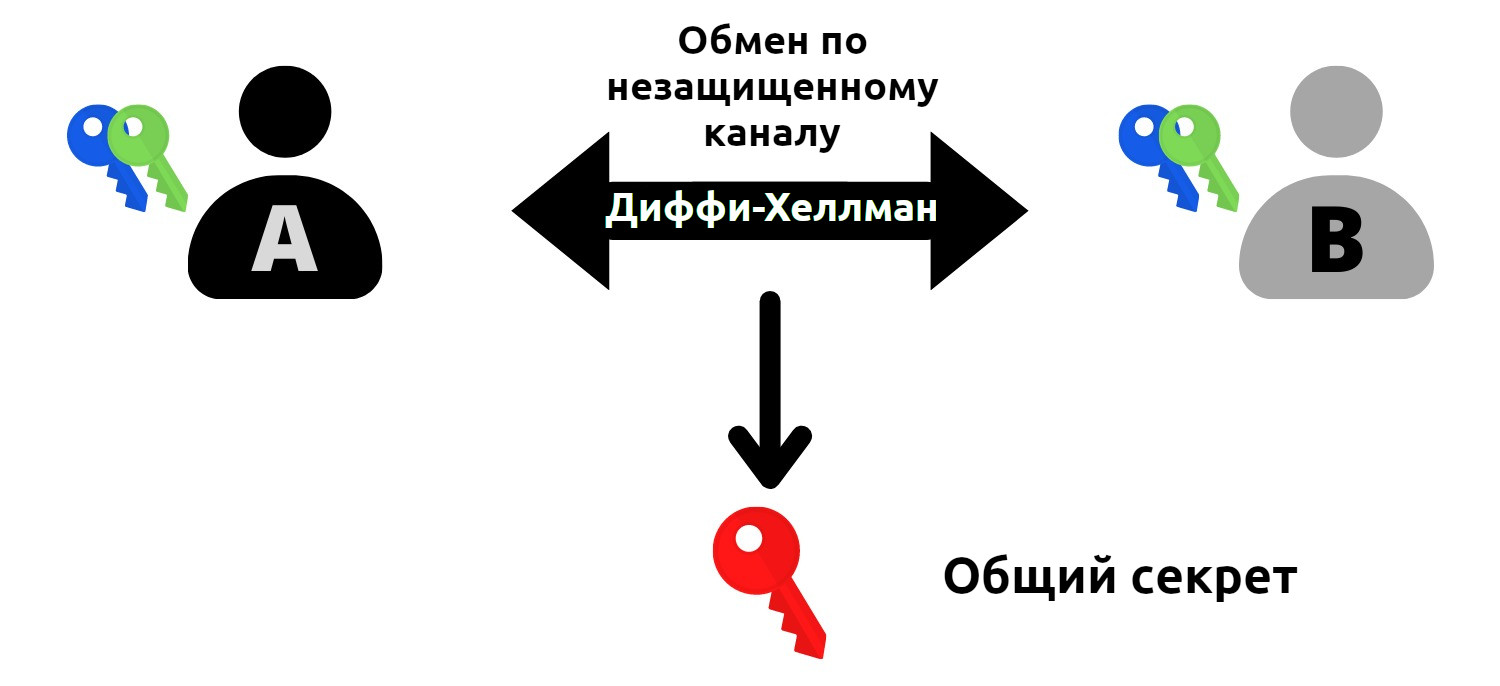
Этот общий секрет (красный ключ) может быть использован для выполнения других задач. Как правило, этот общий секрет может использоваться для шифрования и дешифрования сообщений в незащищенной сети:

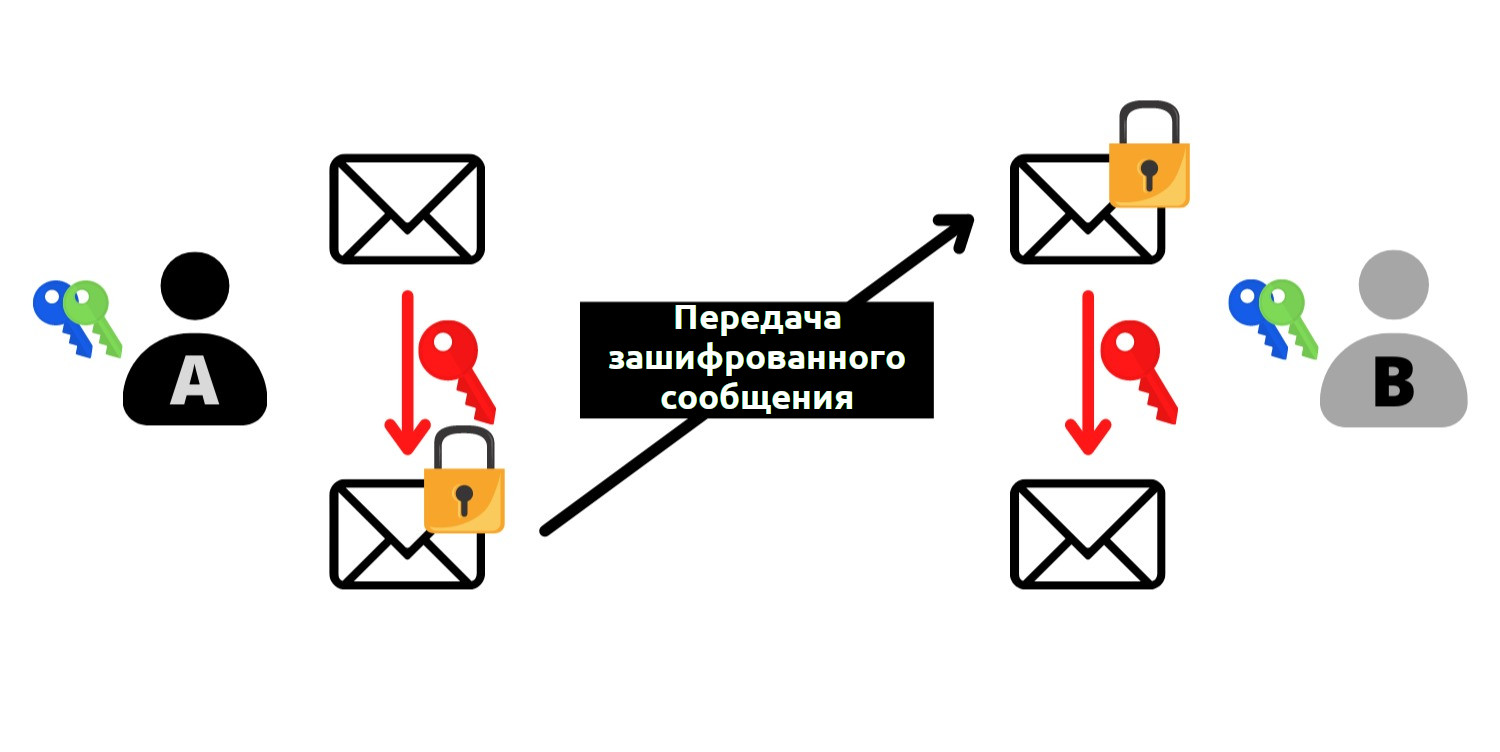
Для достижения такого обмена Диффи-Хеллман использует модульную арифметику для вычисления общего секрета. Вот как это работает в простых терминах:

Алиса и Боб определяют общий цвет, в данном случае желтый. Этот цвет известен всем. Это открытые данные.
Алиса выбирает секретный цвет, в данном случае красный. Она смешивает два цвета, в результате чего получается оранжевый.
Боб выбирает секретный цвет, в данном случае синий. Он смешивает два цвета, в результате чего получает небесно-голубой.
Алиса и Боб могут обменяться полученными цветами: оранжевым и небесно-голубым. Этот обмен может происходить в незащищенной сети и наблюдаться злоумышленниками.
Алиса смешивает полученный от Боба небесно-голубой цвет со своим секретным цветом (красным). Она получает коричневый цвет.
Боб смешивает оранжевый цвет, полученный от Алисы, со своим секретным цветом (небесно-голубым). Он получает тот же коричневый цвет.

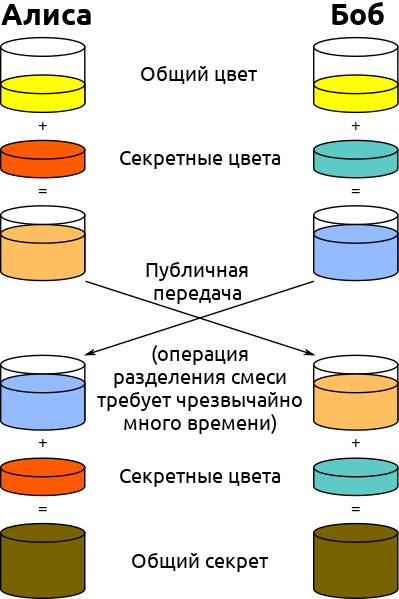
В этом примере коричневый цвет представляет собой секрет, которым поделились Алиса и Боб. Нужно понимать, что в реальности злоумышленнику невозможно отделить оранжевый и голубой цвета, чтобы найти секретные цвета Алисы или Боба.

Теперь давайте рассмотрим, как это работает на самом деле. На первый взгляд, принцип Диффи-Хеллмана кажется сложным для понимания. На самом деле, принцип его работы - почти детская игра. Прежде чем подробно рассказать о его механизмах, напомню два математических понятия, которые нам понадобятся (и которые, кстати, используются и во многих других криптографических методах).

Простое число - это натуральное число, которое имеет только два делителя: 1 и само себя. Например, число 7 является простым, поскольку оно может делиться только на 1 и на 7 (само на себя). С другой стороны, число 8 не является простым, поскольку оно может делиться на 1, 2, 4 и 8. Таким образом, у него не два делителя, а четыре целых положительных делителя.
“Модуль” (также известный как “mod” или “%”) - это математическая операция над двумя целыми числами, которая возвращает остаток от евклидова деления первого числа на второе. Например, 16 mod 5 равно 1.

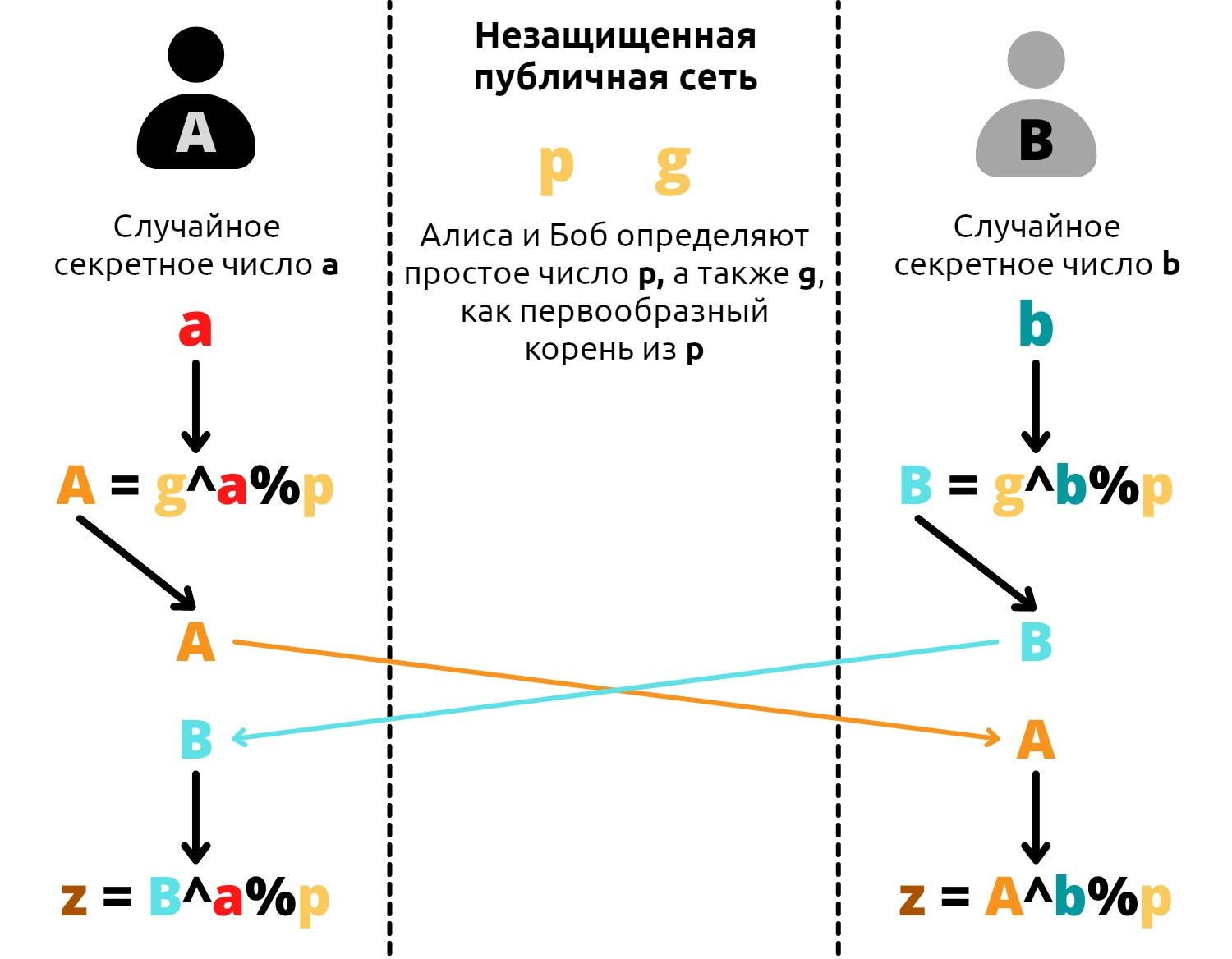
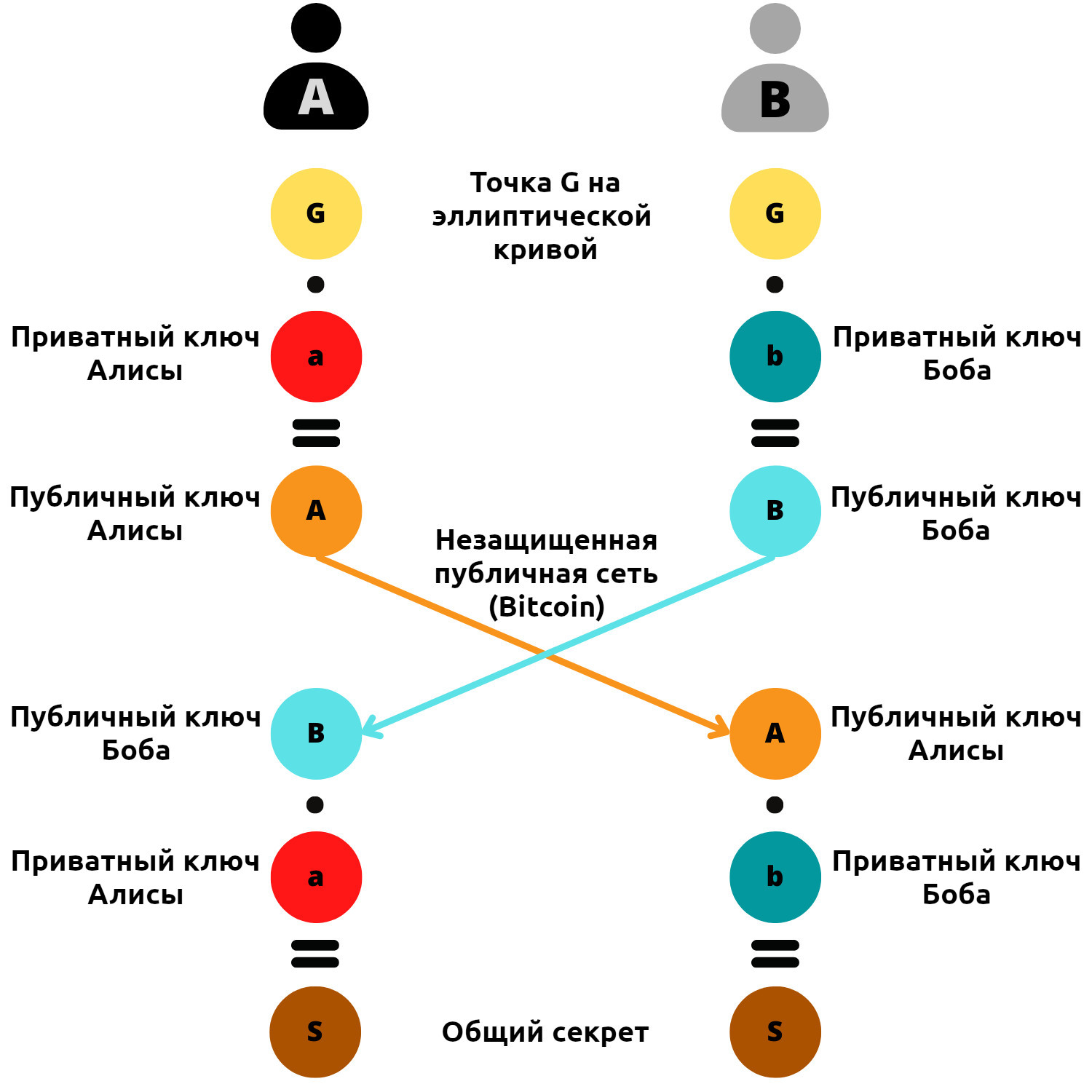
Обмен ключами по протоколу Диффи-Хеллмана между Алисой и Бобом происходит следующим образом:

Алиса и Боб определяют два общих числа: p и g. p - простое число. Чем больше число p, тем надежнее защита Диффи-Хеллмана. g - первообразный корень из p. Эти два числа могут быть переданы открытым текстом по незащищенной сети; они эквивалентны желтому цвету в приведенном выше примере. Алиса и Боб просто должны иметь одинаковые значения p и g.
После того как параметры выбраны, Алиса и Боб определяют секретное случайное число. Случайное число, полученное Алисой, называется a (эквивалентно красному цвету), а случайное число, полученное Бобом, называется b (эквивалентно синему цвету). Эти два числа должны оставаться в секрете.
Вместо того чтобы обмениваться этими числами a и b, каждая сторона вычислит A (заглавная буква) и B (заглавная буква) следующим образом:

# A равно g в степени a по модулю p:
A = g^a % p 

# B равно g в степени b по модулю p:
B = g^b % p

Эти числа A (эквивалент оранжевого цвета) и B (эквивалент небесно-голубого цвета) будут переданы сторонами друг другу. Обмен может происходить открытым текстом в незащищенной сети.
Алиса, которой теперь известно число B, вычислит значение z, следующим образом:

# z равно B в степени a по модулю p: 
z = B^a % p

Напомним, что B = g^b % p. Таким образом:

z = B^a % p
z = (g^b)^a % p

# В соответствии с правилами вычисления степеней:
(x^n)^m = x^nm

# Получаем:
z = g^ba % p

Боб, который теперь знает A, также вычислит значение z, следующим образом:

# z равно A в степени b по модулю p:
z = A^b % p
 
# Получаем:
z = (g^a)^b % p
z = g^ab % p
z = g^ba % p

Таким образом, Алиса и Боб находят совершенно одинаковое значение z. Это число представляет собой их общий секрет, т.е. эквивалент коричневого цвета в нашем примере. Они могут использовать этот общий секрет для шифрования сообщения между ними в незащищенной сети.

Злоумышленник, владеющий p, g, A и B, не сможет вычислить a, b или z. Это было бы равносильно обращению экспоненты вспять. Такое вычисление невозможно провести иначе, чем перебирая все возможности по очереди, поскольку мы работаем с конечным полем. Это было бы похоже на вычисление дискретного логарифма, т.е. обратного экспоненте в конечной циклической группе.

Таким образом, при достаточно больших значениях a, b и p метод Диффи-Хеллмана безопасен. При параметрах в 2048 бит (число из 600 десятичных цифр) проверить все возможности для a и b нереально. На сегодняшний день при числах такого размера алгоритм считается безопасным.

Именно в этом и заключается основной недостаток протокола Диффи-Хеллмана. Чтобы быть безопасным, алгоритм должен использовать большие числа. Поэтому сегодня мы предпочитаем использовать ECDH-вариант алгоритма Диффи-Хеллмана, использующий алгебраическую кривую, в данном случае эллиптическую. Это позволит нам работать с гораздо меньшими числами при сохранении эквивалентной безопасности, а значит, сократить ресурсы, необходимые для вычислений и хранения.

Общий принцип работы алгоритма остается прежним. Однако вместо случайного числа a и числа A, вычисляемого из a с помощью модульного экспонирования, мы будем использовать пару ключей, созданных на эллиптической кривой. Вместо того чтобы опираться на дистрибутивность оператора модуля, мы будем использовать групповой закон для эллиптических кривых, а точнее, ассоциативность этого закона.

Если говорить кратко, то приватный ключ - это случайное число от 1 до n-1 (n - порядок кривой), а публичный ключ - уникальная точка на кривой, определяемая с помощью приватного ключа путем сложения и удвоения точек из порождающей точки следующим образом:

K = k·G

Где K - публичный ключ, k - приватный ключ, а G - точка-генератор.

Одно из свойств этой пары ключей заключается в том, что очень легко определить K, зная k и G, но невозможно определить k, зная K и G. Это односторонняя функция.

Другими словами, легко вычислить публичный ключ, если известен приватный ключ, но невозможно вычислить приватный ключ, если известен публичный ключ. И снова эта безопасность основана на невозможности вычисления дискретного логарифма.

Это свойство мы будем использовать для адаптации нашего алгоритма Диффи-Хеллмана. Принцип работы ECDH заключается в следующем:

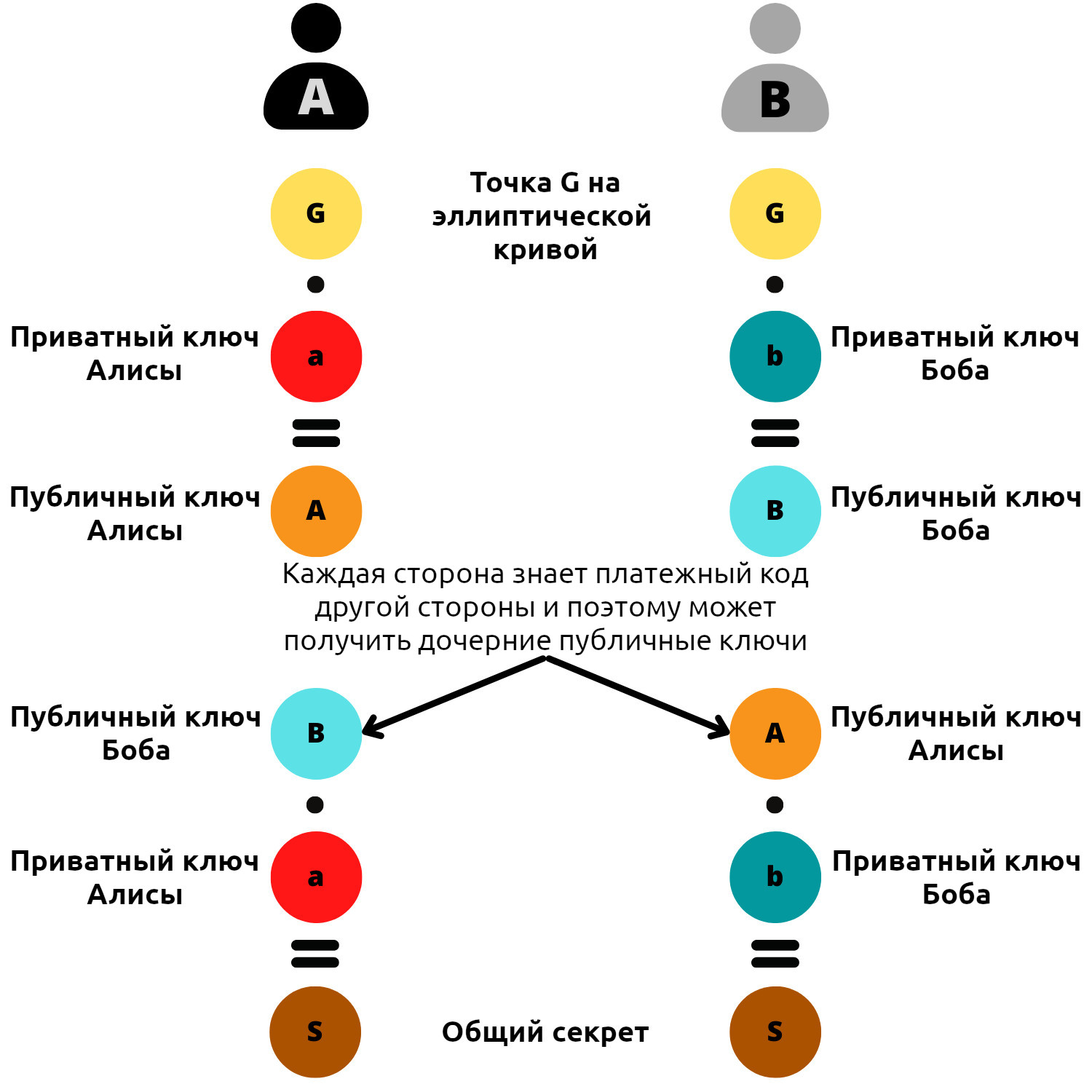
Алиса и Боб совместно договариваются о криптографически защищенной эллиптической кривой и ее параметрах. Эта информация является общедоступной.
Алиса генерирует случайное число ka, которое будет ее приватным ключом. Этот приватный ключ должен оставаться в секрете. Свой публичный ключ Ka она определяет путем сложения и удвоения точек на выбранной эллиптической кривой.

Ka = ka·G

Боб также генерирует случайное число, которое будет его приватным ключом kb. И вычисляет связанный с ним публичный ключ Kb.

Kb = kb·G

Алиса и Боб обмениваются своими публичными ключами Ka и Kb в незащищенной сети общего пользования.
Алиса вычисляет точку (x,y) на кривой, применяя свой приватный ключ ka к публичному ключу Боба Kb.

(x,y) = ka·Kb

Боб вычисляет точку (x,y) на кривой, применяя свой приватный ключ kb к публичному ключу Алисы Ka.

(x,y) = kb·Ka

Алиса и Боб получают одну и ту же точку на эллиптической кривой. Общий секрет будет представлять собой координату x этой точки.

Они получают один и тот же общий секрет, потому что:

(x,y) = ka·Kb = ka·kb·G = kb·ka·G = kb·Ka

Злоумышленник, наблюдающий за незащищенной общедоступной сетью, сможет получить только публичные ключи сторон и параметры выбранной кривой. Как было сказано выше, эти две части информации сами по себе не могут быть использованы для определения приватных ключей, поэтому злоумышленник не сможет получить доступ к секрету.

Таким образом, ECDH является алгоритмом обмена ключами. Он часто используется наряду с другими криптографическими методами для определения протокола. Например, ECDH лежит в основе TLS (Transport Layer Security) - протокола шифрования и аутентификации, используемого на транспортном уровне Интернета. В TLS для обмена ключами используется ECDHE - вариант ECDH, в котором ключи являются эфемерными, чтобы обеспечить постоянную конфиденциальность. Помимо ECDH, в TLS также используются алгоритм аутентификации ECDSA, алгоритм шифрования AES и хеш-функция SHA256.

В частности, TLS определяет букву “s” в слове “https”, а также маленький замочек, который вы видите на экране браузера в левом верхнем углу, гарантирующий, что обмен данными зашифрован. Таким образом, читая эту статью, вы используете ECDH, и, возможно, вы используете его каждый день, даже не подозревая об этом.

Транзакция уведомления #

Как мы выяснили в предыдущем разделе, ECDH - это вариант протокола Диффи-Хеллмана с использованием пар ключей, созданных на эллиптической кривой. И хорошо, что в наших кошельках Bitcoin есть множество пар ключей, соответствующих этому стандарту!

Идея заключается в том, чтобы использовать пары ключей иерархических детерминированных кошельков Bitcoin двух участвующих сторон для создания общих и эфемерных секретов между ними. В BIP47 вместо этого используется ECDHE (Elliptic Curve Diffie-Hellman Ephemeral).

ECDHE используется в BIP47 для передачи платежного кода от отправителя к получателю. Это и есть транзакция уведомления. Фактически для использования BIP47 каждая из двух сторон (отправитель, отправляющий платежи, и получатель, получающий платежи) должна знать платежный код другой стороны. Это необходимо для получения эфемерных публичных ключей, а значит, и выделенных адресов получения.

До обмена платежными кодами отправитель уже знает платежный код получателя, поскольку он мог найти его вне блокчейна, например, на сайте получателя или в социальных сетях. Однако получатель не обязательно знает платежный код отправителя. Его необходимо сообщить, иначе получатель не сможет получить свои эфемерные ключи, а значит, не сможет узнать, где находятся его биткоины, и потратить свои средства. Мы могли бы отправить платежный код вне блокчейна, используя другую систему связи, но это создаст проблему, если кошелек будет восстановлен из сида.

Это связано с тем, что, как я уже отмечал, адреса BIP47 получаются не из сида получателя (иначе можно было бы использовать один из xpub напрямую), а в результате вычисления двух платежных кодов: получателя и отправителя. Именно поэтому, если получатель потеряет свой кошелек и попытается восстановить его по своему сиду, ему обязательно понадобятся все платежные коды тех, кто отправил ему биткоины через BIP47.

Можно было бы легко использовать BIP47 без этой уведомительной транзакции, но при этом каждый пользователь должен был бы создавать резервные копии платежных кодов своих контрагентов. Эта ситуация будет оставаться таковой до тех пор, пока мы не найдем простой и надежный способ создания, хранения и обновления таких резервных копий. Поэтому в настоящее время транзакция уведомления является практически обязательной.

Как следует из названия, эта операция не только передает платежный код, но и выполняет функцию оповещения получателя. Она уведомляет получателя о том, что платежный канал только что был открыт.

Прежде чем более подробно рассказать о технической стороне транзакции уведомления, я хотел бы немного остановиться на модели конфиденциальности. Модель BIP47 предусматривает некоторые меры предосторожности, принятые при построении этой начальной транзакции.

Сам по себе платежный код не представляет непосредственного риска потери конфиденциальности. В отличие от классической модели Bitcoin, в которой связь между личностью пользователя и транзакциями разрывается, в частности, за счет анонимности публичных ключей, платежный код может быть напрямую связан с личностью. Очевидно, что это не является обязательным условием, но такая связь не представляет опасности.

Это связано с тем, что платежный код не является непосредственным источником адресов, используемых для получения платежей BIP47. Вместо этого адреса получаются путем применения ECDHE между дочерними ключами платежных кодов двух сторон.

Таким образом, сам по себе платежный код не представляет прямого риска потери конфиденциальности, поскольку из него может быть получен только адрес для уведомления. Из него можно получить некоторую информацию, но узнать, с кем вы совершаете сделку, обычно не представляется возможным.

Поэтому очень важно поддерживать строгое разделение между платежными кодами пользователей. При этом первоначальное сообщение кода является критическим моментом для обеспечения конфиденциальности платежа, и в то же время оно необходимо для корректной работы протокола. Если один из двух платежных кодов может быть получен публично (например, с веб-сайта), то второй код, т.е. код отправителя, не должен быть связан с первым.

Допустим, я хочу сделать пожертвование с помощью BIP47 на мирное протестное движение дальнобойщиков в Канаде:

Эта организация опубликовала свой платежный код непосредственно на своем сайте или в социальных сетях.
Таким образом, этот код ассоциируется с протестным движением.
Я так же имею публичный платежный код.
Прежде чем отправить им транзакцию, я должен убедиться, что они знают мой персональный платежный код, который также связан с моей личностью, поскольку я использую его для получения транзакций в своих социальных сетях.

Как я могу отправить его им? Если я отправлю его им с помощью обычных средств связи, есть риск, что информация просочится, и меня запишут в сторонники протестного движения.

Конечно, транзакция с уведомлением не является единственным решением для скрытой передачи платежного кода отправителя, но на данный момент она прекрасно справляется с этой ролью, применяя несколько уровней защиты.

На приведенной ниже диаграмме красные линии обозначают момент, когда информационный поток должен быть прерван, а черные стрелки - неоспоримые связи, которые может установить сторонний наблюдатель:

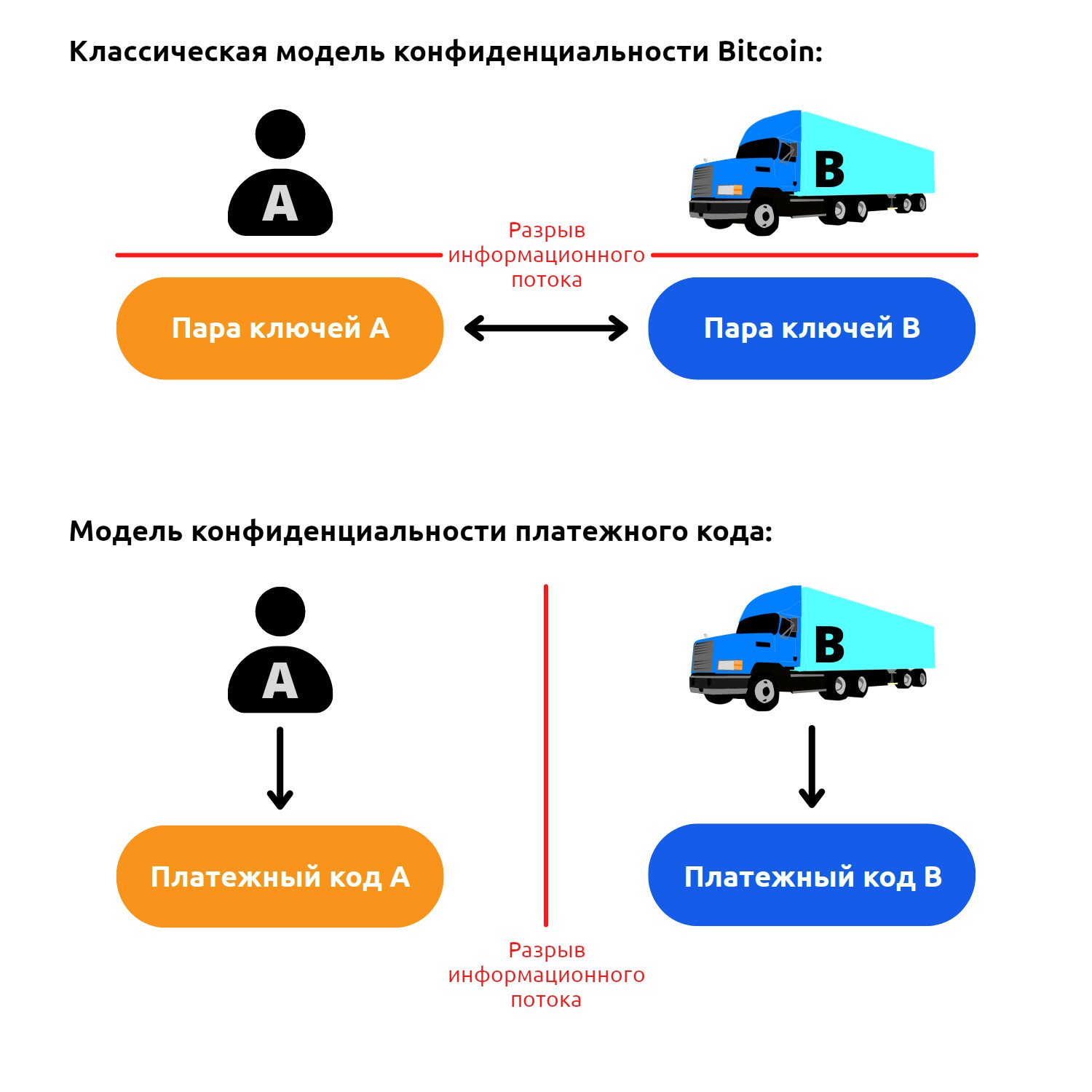
В действительности для классической модели конфиденциальности Bitcoin зачастую сложно полностью прервать информационный поток между ключевой парой и пользователем, особенно при удаленном совершении транзакций. Например, в случае кампании по сбору пожертвований получатель будет вынужден раскрыть публичный адрес или публичный ключ на своем сайте или в социальных сетях. Использование BIP47 с транзакцией уведомления решает эту проблему благодаря ECDHE и слою шифрования, который мы будем изучать.

Очевидно, что классическая модель конфиденциальности Bitcoin по-прежнему соблюдается на уровне эфемерных публичных ключей, получаемых в результате комбинации двух платежных кодов. Эти две модели взаимозависимы. Я просто хочу подчеркнуть, что, в отличие от классического использования публичного ключа для получения биткоинов, платежный код может быть связан с личностью, поскольку информация “Боб совершает транзакцию с Алисой” нарушается в другое время. Платежный код используется для генерации платежных адресов, но, наблюдая только за блокчейном, невозможно связать платежную транзакцию BIP47 с платежными кодами, которые использовались для ее проведения.

Построение транзакции уведомления #

Теперь посмотрим, как работает эта транзакция уведомления. Представим, что Алиса хочет отправить деньги Бобу, используя BIP47. В моем примере Алиса выступает в роли отправителя, а Боб - в роли получателя. Боб опубликовал свой платежный код на своем сайте. Поэтому Алиса уже знает платежный код Боба.

Алиса вычисляет общий секрет с помощью ECDH:

Она выбирает из своего HD-кошелька пару ключей, которая находится на другой ветке, отличной от той, где находится ее платежный код. Обратите внимание, что эта пара не должна легко ассоциироваться ни с адресом уведомления Алисы, ни с ее личностью (см. предыдущий раздел).
Алиса берет приватный ключ из этой пары. Мы назовем его “a” (в нижнем регистре).

Алиса извлекает публичный ключ, связанный с адресом уведомления Боба. Этот ключ - первый дочерний ключ, полученный из платежного кода Боба (индекс 0). Мы называем этот публичный ключ “B” (заглавная буква). Приватный ключ, связанный с этим публичным ключом, называется “b” (строчная буква). “B” определяется путем сложения и удвоения точек на эллиптической кривой, начиная с “G” (порождающей точки) и заканчивая “b” (приватным ключом).

B = b·G

Алиса вычисляет секретную точку “S” (верхний регистр) на эллиптической кривой путем сложения и удвоения точек, применяя свой приватный ключ “a” к публичному ключу Боба “B”.

S = a·B

Алиса вычисляет коэффициент ослепления “f”, который будет использоваться для шифрования ее платежного кода. Для этого она использует функцию HMAC-SHA512 для определения псевдослучайного числа. Вторым входом этой функции является значение, которое сможет найти Боб: (x), которое является абсциссой секретной точки, вычисленной ранее. Первым входом является (o) - UTXO, используемый в качестве входа в данную транзакцию.

f = HMAC-SHA512(o, x)

Алиса переводит свой личный платежный код в основание 2 (двоичное).
Она использует этот ослепляющий фактор в качестве ключа для выполнения симметричного шифрования содержимого своего платежного кода. Используемый алгоритм шифрования представляет собой простое XOR. Выполняемая операция сравнима с шифром Вернама, известным также как “одноразовый блокнот”:

Сначала Алиса делит свой коэффициент ослепления на две части: первые 32 байта называются “f1”, а последние 32 байта - “f2”. Получаем:

f = f1 || f2

Алиса отдельно вычисляет шифротекст (x’) публичного ключа (x) своего платежного кода и шифротекст (c’) своего кода цепочки (chain code) (c). В качестве ключей шифрования выступают соответственно “f1” и “f2”. Используется операция XOR (исключающее “или”).

x' = x XOR f1
c' = c XOR f2

Алиса заменяет реальные значения абсциссы публичного ключа (x) и кода цепочки (c) в своем платежном коде на зашифрованные значения (x’) и (c’).

Прежде чем продолжить техническое описание этой транзакции уведомления, рассмотрим операцию XOR. XOR - это побитовый логический оператор, основанный на булевой алгебре. При задании двух операндов в битах он возвращает 1, если биты одинакового ранга различны, и 0, если биты одинакового ранга равны. Приведем таблицу истинности XOR в зависимости от значений операндов D и E:

D	E	D XOR E
0	0	0
0	1	1
1	0	1
1	1	0

Например:

0110 XOR 1110 = 1000

Или:

010011 XOR 110110 = 100101

В ECDH использование XOR в качестве уровня шифрования особенно органично. Во-первых, благодаря этому оператору шифрование является симметричным. Это означает, что получатель может расшифровать код платежа с помощью того же ключа, который использовался для шифрования. Ключи шифрования и дешифрования вычисляются из общего секрета с помощью ECDH.

Такая симметрия возможна благодаря свойствам коммутативности и ассоциативности оператора XOR:

 # Прочие свойства:
 -> D ⊕ D = 0
 -> D ⊕ 0 = D
 
 # Коммутативность:
 D ⊕ E = E ⊕ D
 
 # Ассоциативность:
 D ⊕ (E ⊕ Z) = (D ⊕ E) ⊕ Z = D ⊕ E ⊕ Z
 
 # Симметричность:
 Если: D ⊕ E = L
 То:   D ⊕ L = D ⊕ (D ⊕ E) = D ⊕ D ⊕ E = 0 ⊕ E = E
 ->  D ⊕ L = E

Во-вторых, этот метод шифрования очень похож на шифр Вернама (одноразовый блокнот) - единственный известный на сегодняшний день алгоритм шифрования, обладающий безусловной (или абсолютной) безопасностью. Для того чтобы шифр Вернама обладал такими свойствами, ключ шифрования должен быть совершенно случайным, иметь размер, равный размеру сообщения, и использоваться только один раз. В используемом здесь методе шифрования BIP47 ключ имеет размер, равный размеру сообщения, а коэффициент ослепления равен конкатенации абсциссы публичного ключа с “chain code” платежного кода. Такой ключ шифрования используется только один раз. Однако этот ключ не является производным от совершенной случайности, поскольку он представляет собой HMAC. Вместо этого он является псевдослучайным. Таким образом, это не шифр Вернама, но метод близок к нему.

Вернемся к построению транзакции уведомления:

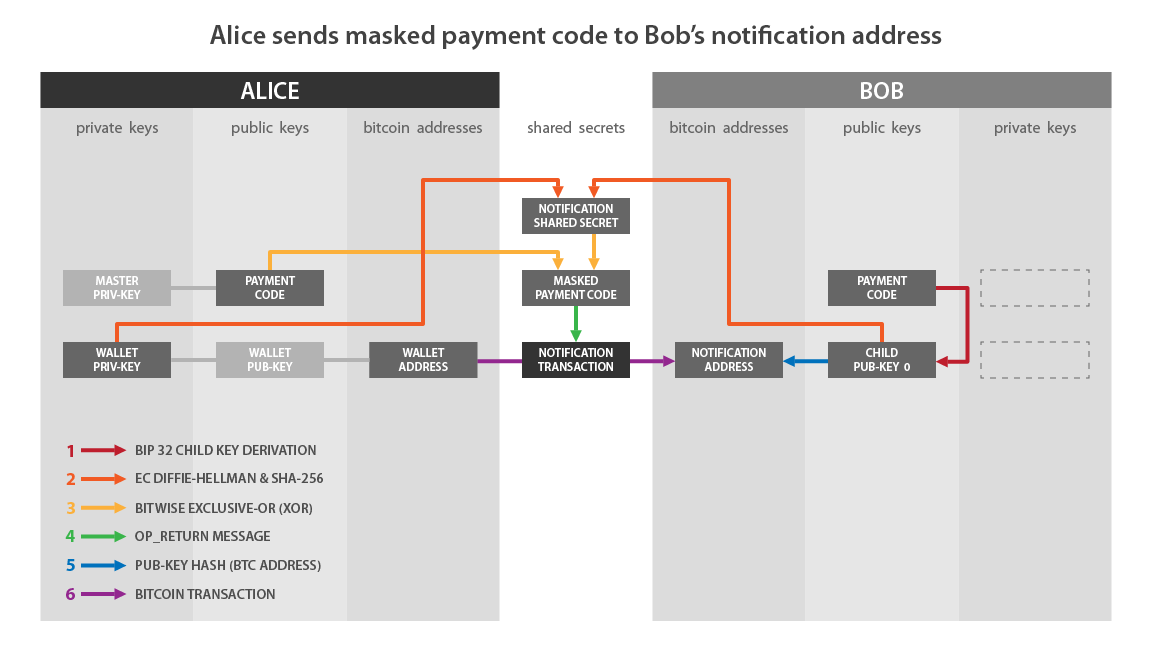
Таким образом, Алиса в настоящее время имеет свой платежный код с зашифрованной полезной нагрузкой. Она собирается построить и передать транзакцию, в которой на входе будет ее публичный ключ “A”, на выходе - адрес уведомления Боба, а в выходе OP_RETURN - ее платежный код с зашифрованной полезной нагрузкой. Эта транзакция является транзакцией уведомления.

OP_RETURN - это “opcode”, т.е. скрипт, который помечает вывод транзакции Bitcoin как нерасходуемый. Сегодня он используется для трансляции и закрепления информации в блокчейне Bitcoin. В нем может храниться до 80 байт данных, которые затем записываются в блокчейн и становятся видны всем остальным пользователям.

Как мы видели в предыдущем разделе, алгоритм Диффи-Хеллмана используется для создания секрета, который передается двум пользователям, общающимся по незащищенной сети и потенциально наблюдаемым злоумышленниками. В BIP47 ECDH используется для связи в сети Bitcoin, которая по своей природе является прозрачной сетью, наблюдаемой многими злоумышленниками. Общий секрет, вычисленный с помощью обмена ключами Диффи-Хеллмана на эллиптической кривой, затем используется для шифрования передаваемой секретной информации: платежного кода отправителя (Алисы).

Приведем схему из BIP47, которая иллюстрирует то, что мы только что описали:

Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Если сопоставить эту схему с тем, что я описал ранее, то:

“Wallet Priv-Key” на стороне Алисы соответствует: a.
“Child Pub-Key 0” на стороне Боба соответствует: B.
“Notification Shared Secret” соответствует: f.
“Masked Payment Code” соответствует замаскированному платежному коду, т.е. с зашифрованной полезной нагрузкой: x’ и c’.
“Notification Transaction” - это транзакция, содержащая OP_RETURN.

Я обобщу только что рассмотренные нами шаги по проведению транзакции уведомления:

Алиса получает платежный код и адрес уведомления Боба.
Алиса выбирает из своего HD-кошелька принадлежащий ей UTXO с соответствующей парой ключей.
Она вычисляет секретную точку на эллиптической кривой с помощью ECDH.
Она использует эту секретную точку для вычисления HMAC, который является коэффициентом ослепления.
Она использует этот ослепляющий фактор для шифрования полезной нагрузки своего персонального платежного кода.
Для передачи замаскированного платежного кода Бобу используется выход OP_RETURN в транзакции уведомления.

Для того чтобы более подробно понять, как это работает, и в частности, как используется OP_RETURN, рассмотрим реальную транзакцию уведомления. Подобную транзакцию я проводил в Testnet, с которой можно ознакомиться по ссылке.

TXID:

0e2e4695a3c49272ef631426a9fd2dae6ec3a469e3a39a3db51aa476cd09de2e

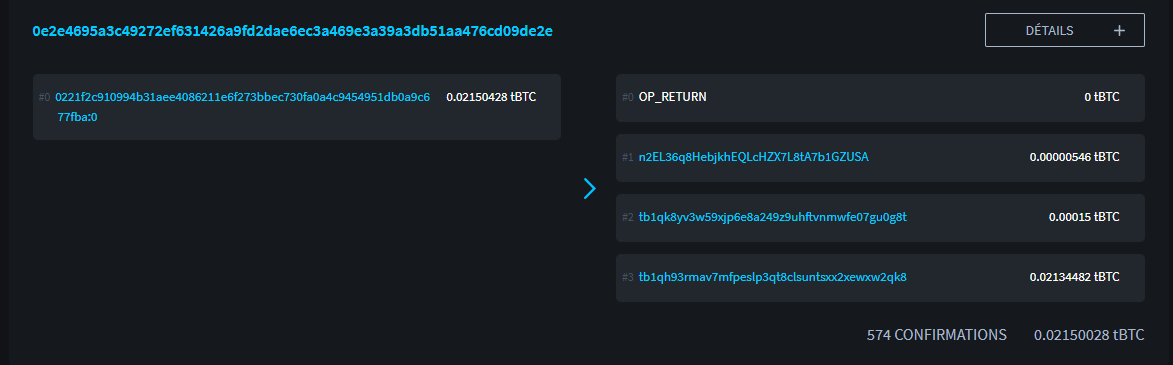
Источник: https://blockstream.info/

Рассматривая эту транзакцию, мы видим, что она имеет один вход и 4 выхода:

Первый выход - OP_RETURN, который содержит мой скрытый платежный код.
Второй выход на 546 сатоши указывает на адрес уведомления моего получателя.
Третий вывод в размере 15 000 сат представляет собой комиссию, поскольку для проведения этой транзакции я использовал кошелек Samourai Wallet.
Четвертый выход на два миллиона сатоши представляет собой сдачу, т.е. оставшуюся разницу из моего входа, которая возвращается на другой принадлежащий мне адрес.

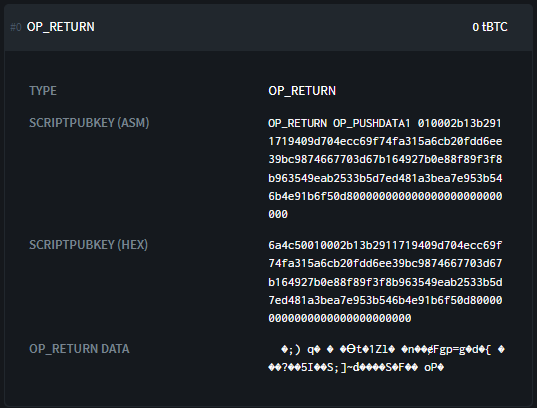
Наиболее интересным для изучения, очевидно, является выход 0 с OP_RETURN. Рассмотрим подробнее, что он содержит:

Источник: https://blockstream.info/

Выходной скрипт в шестнадцатеричном виде:

6a4c50010002b13b2911719409d704ecc69f74fa315a6cb20fdd6ee39bc9874667703d67b164927b0e88f89f3f8b963549eab2533b5d7ed481a3bea7e953b546b4e91b6f50d800000000000000000000000000

Этот скрипт состоит из нескольких частей:

6a4c50010002b13b2911719409d704ecc69f74fa315a6cb20fdd6ee39bc9874667703d67b164927b0e88f89f3f8b963549eab2533b5d7ed481a3bea7e953b546b4e91b6f50d800000000000000000000000000

Опкоды: 6a4c
Байт, указывающий размер сообщения (80 байт): 50
Метаданные моего незашифрованного платежного кода: 010002
Зашифрованная абсцисса публичного ключа моего платежного кода: b13b2911719409d704ecc69f74fa315a6cb20fdd6ee39bc9874667703d67b164
Зашифрованный код цепочки (chain code) моего платежного кода: 927b0e88f89f3f8b963549eab2533b5d7ed481a3bea7e953b546b4e91b6f50d8
Дополнение для достижения 80 байт: 00000000000000000000000000

Опкоды включают 0x6a для OP_RETURN и 0x4c для OP_PUSHDATA1. Байт, следующий за этим последним опкодом, указывает на размер последующей полезной нагрузки. Он указывает на 0x50, т.е. 80 байт.

Далее следует платежный код с зашифрованной полезной нагрузкой.

Вот мой незашифрованный платежный код, использованный в этой операции:

В base 58: PM8TJQCyt6ovbozreUCBrfKqmSVmTzJ5vjqse58LnBzKFFZTwny3KfCDdwTqAEYVasn11tTMPc2FJsFygFd3YzsHvwNXLEQNADgxeGnMK8Ugmin62TZU
В base 16 (HEX): 4701000277507c9c17a89cfca2d3af554745d6c2db0e7f6b2721a3941a504933103cc42add94881210d6e752a9abc8a9fa0070e85184993c4f643f1121dd807dd556d1dc000000000000000000000000008604e4db

Если сравнить мой незашифрованный код платежа с OP_RETURN, то видно, что HRP (коричневый цвет) и контрольная сумма (розовый цвет) не передаются. Это нормально, так как эта информация предназначена для человека.

Далее мы можем узнать (зеленым цветом) версию (0x01), битовое поле (0x00) и четность публичного ключа (0x02). И в конце платежного кода - пустые байты черного цвета (0x00), которые дополняют количество байт до 80. Все эти метаданные передаются в незашифрованном виде.

Наконец, мы видим, что абсцисса публичного ключа (синий цвет) и код цепочки (красный цвет) зашифрованы. Это и есть полезная нагрузка платежного кода.

Получение транзакции уведомления #

Теперь, когда Алиса отправила Бобу транзакцию уведомления, посмотрим, как Боб ее интерпретирует.

Напомним, что Боб должен иметь доступ к платежному коду Алисы. Без этой информации, как мы увидим в следующем разделе, он не сможет вывести ключевые пары, созданные Алисой, а значит, не сможет получить доступ к своим биткоинам, полученным с помощью BIP47. На данный момент полезная нагрузка платежного кода Алисы зашифрована. Посмотрим, как Боб его расшифрует.

Боб отслеживает транзакции, создающие выходы с его адресом уведомления.
Когда транзакция имеет выход на адресе уведомления, Боб анализирует ее на предмет наличия в ней выхода OP_RETURN, соответствующего стандарту BIP47.
Если первый байт полезной нагрузки OP_RETURN равен 0x01, то Боб начинает поиск возможного секрета, совместно используемого с ECDH:

Боб выбирает публичный ключ из транзакции в качестве входного. Это публичный ключ Алисы с именем “A”:

A = a·G

Боб выбирает приватный ключ “b”, связанный с его личным адресом уведомления:

Боб вычисляет секретную точку “S” (общий секрет ECDH) на эллиптической кривой путем сложения и удвоения точек, применяя свой приватный ключ “b” к публичному ключу Алисы “A”:

S = b·A

Боб определяет коэффициент ослепления “f”, который позволит расшифровать полезную нагрузку платежного кода Алисы. Аналогично тому, как Алиса вычислила его ранее, Боб найдет “f”, применив HMAC-SHA512 к (x) - значению абсциссы секретной точки “S”, и к (o) - UTXO, используемому в качестве входа в эту транзакцию уведомления:

f = HMAC-SHA512(o, x)

Боб интерпретирует данные OP_RETURN в транзакции уведомления как платежный код. Он просто расшифрует полезную нагрузку этого потенциального кода платежа, используя коэффициент ослепления “f”:

Боб разбивает коэффициент ослепления “f” на две части: первые 32 байта “f” будут “f1”, а последние 32 байта - “f2”.
Боб расшифровывает значение зашифрованной абсциссы (x’) публичного ключа платежного кода Алисы:

x = x' XOR f1

Боб расшифровывает значение кода цепочки (c’) в платежном коде Алисы:

c = c' XOR f2

Боб проверяет, входит ли значение публичного ключа платежного кода Алисы в группу secp256k1. Если да, то он интерпретирует его как действительный платежный код. В противном случае он игнорирует транзакцию.

Теперь, когда Боб знает код платежа Алисы, Алиса может послать ему до 2^32 платежей, не повторяя ни разу транзакцию уведомления.

Почему это работает? Как Бобу удается определить тот же коэффициент ослепления, что и Алисе, и, следовательно, расшифровать ее платежный код? Рассмотрим подробнее действие ECDH в описанном выше контексте.

Прежде всего, мы имеем дело с симметричным шифрованием. Это означает, что ключ шифрования и ключ дешифрования являются одним и тем же значением. Таким ключом в транзакции уведомления является коэффициент ослепления (f = f1 || f2). Поэтому Алисе и Бобу необходимо получить одно и то же значение для f, не передавая его напрямую, так как злоумышленник может украсть его и расшифровать секретную информацию.

Этот коэффициент ослепления получается путем применения HMAC-SHA512 к двум значениям: абсциссе секретной точки и UTXO, использованному в транзакции. Таким образом, Бобу необходимо иметь эти две части информации, чтобы расшифровать полезную нагрузку платежного кода Алисы.

Что касается UTXO на входе, то Боб может просто получить его, наблюдая за транзакцией уведомления. Для секретной точки Бобу придется использовать ECDH.

Как мы видели в разделе, посвященном Диффи-Хеллману, просто обменявшись публичными ключами и тайно применив свои приватные ключи к публичным ключам друг друга, Алиса и Боб могут найти точную секретную точку на эллиптической кривой. На этом механизме основана транзакция уведомления:

# Пара ключей Боба:
B = b·G

# Пара ключей Алисы:
A = a·G

# Для секретной точки S (x,y):
S = a·B = a·b·G = b·a·G = b·A

Теперь, когда Боб знает код платежа Алисы, он сможет обнаружить ее платежи BIP47 и вывести приватные ключи, блокирующие полученные биткоины.

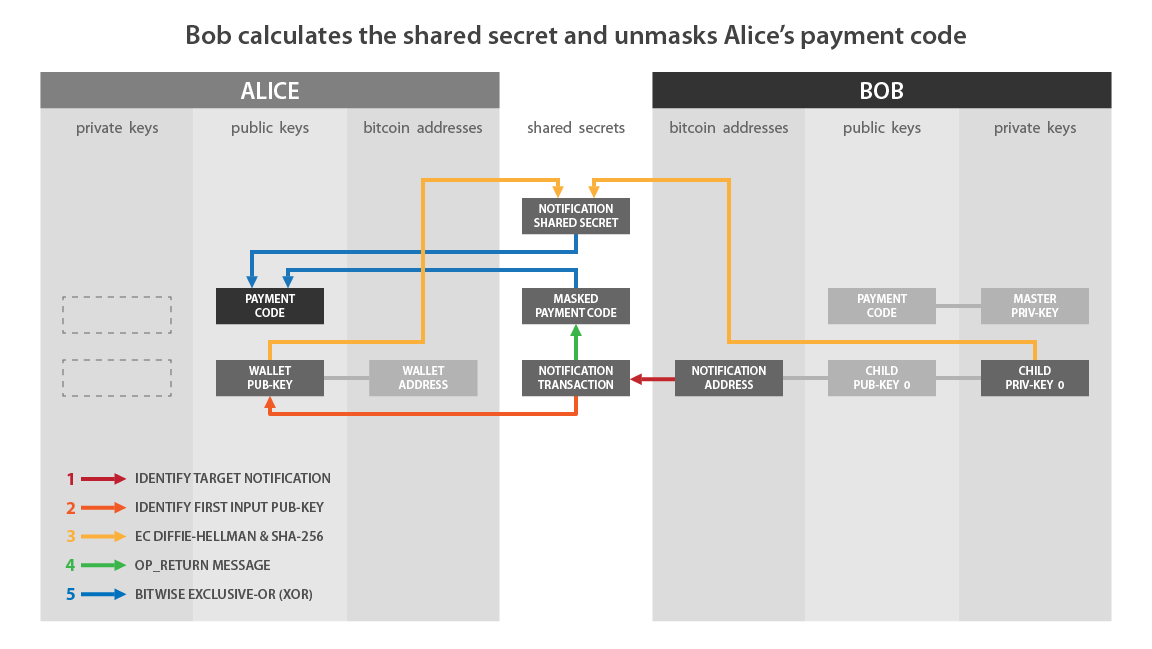
Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Если сопоставить эту схему с тем, что я описал ранее, то:

“Wallet Pub-Key” на стороне Алисы соответствует A.
“Child Priv-Key 0” на стороне Боба соответствует b.
“Notification Shared Secret” соответствует f.
“Masked Payment Code” соответствует замаскированному платежному коду Алисы, т.е. с зашифрованной полезной нагрузкой: x’ и c’.
“Notification Transaction” - это транзакция, содержащая OP_RETURN.

Я подведу итог только что рассмотренным шагам по приему и интерпретации транзакции уведомления:

Боб отслеживает выходы транзакций на свой адрес уведомления.
При обнаружении такового он извлекает информацию, содержащуюся в OP_RETURN.
Боб выбирает публичный ключ в качестве входного и вычисляет секретную точку с помощью ECDH.
Он использует эту секретную точку для вычисления HMAC, который является коэффициентом ослепления.
Он использует этот фактор ослепления для расшифровки полезной нагрузки платежного кода Алисы, содержащегося в OP_RETURN.

Платежная транзакция в рамках BIP47 #

Рассмотрим процесс оплаты с помощью BIP47. Напомним текущую ситуацию :

Алиса знает платежный код Боба, который она просто взяла с его сайта.
Боб знает платежный код Алисы благодаря транзакции уведомления.
Алиса произведет свой первый платеж Бобу. Аналогичным образом она может произвести еще много платежей.

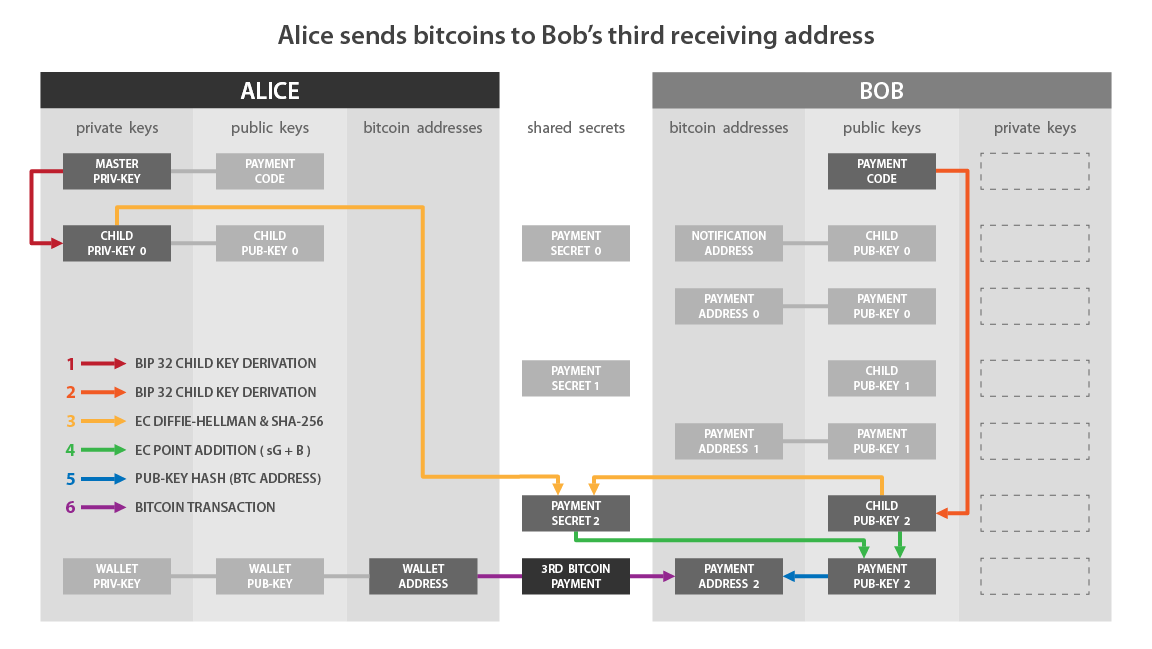
Прежде чем объяснить этот процесс, считаю нужным напомнить, с какими индексами мы сейчас работаем:

Путь деривации для платежного кода описывается следующим образом: m/47’/0’/0’/.

Следующая глубина делит индексы следующим образом:

Первая обычная (не усиленная) дочерняя пара ключей - та, которая используется для генерации адреса уведомления, рассмотренного в предыдущем разделе: m/47’/0’/0’/0/.
Для генерации адресов приема платежей BIP47 в рамках ECDH используются обычные дочерние пары ключей, как мы увидим в этом разделе: m/47’/0’/0’/ от 0 до 2 147 483 647/.
Пары усиленных дочерних ключей представляют собой эфемерные платежные коды: m/47’/0’/0’/ от 0’ до 2 147 483 647’/.

Каждый раз, когда Алиса хочет отправить платеж Бобу, она получает новый уникальный пустой адрес, снова используя протокол ECDH:

Алиса выбирает первый приватный ключ, полученный из ее персонального многоразового платежного кода:

Алиса выбирает первый неиспользованный публичный ключ, полученный из платежного кода Боба. Назовем этот публичный ключ “B”. Он связан с приватным ключом “b”, о котором знает только Боб.

B = b·G

Алиса вычисляет секретную точку “S” на эллиптической кривой путем сложения и удвоения точек, применяя свой приватный ключ “a” к публичному ключу Боба “B”:

S = a·B

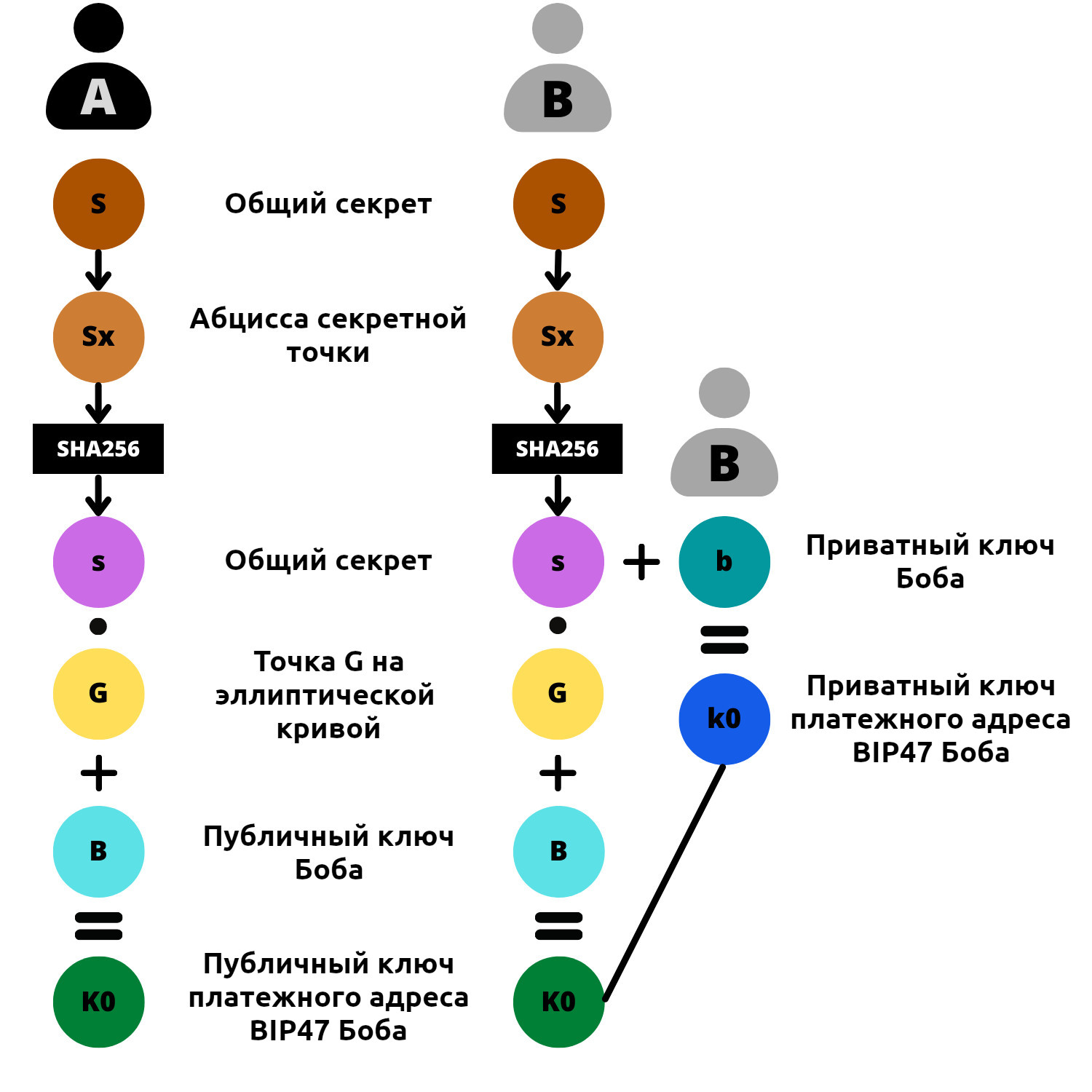
Из этой секретной точки Алиса вычислит общий секрет “s” (в нижнем регистре). Для этого она выбирает абсциссу секретной точки “S”, обозначаемую как “Sx”, и передает это значение хеш-функции SHA256.

s = SHA256(Sx)

Алиса использует этот общий секрет “s” для вычисления адреса приема платежа Bitcoin. Сначала она проверяет, содержится ли “s” в порядке кривой secp256k1. Если это не так, она увеличивает индекс публичного ключа Боба, чтобы получить другой общий секрет.
Во-вторых, она вычисляет публичный ключ “K0” путем сложения точек “B” и “s·G” на эллиптической кривой. Другими словами, Алиса добавляет публичный ключ, полученный из платежного кода Боба “B”, к другой точке, вычисленной на эллиптической кривой путем добавления и удвоения точек с общим секретом “s” из точки “G”, генерирующей кривую secp256k1. Эта новая точка представляет собой публичный ключ, и мы называем ее “K0”:

K0 = B + s·G

С помощью этого публичного ключа “K0” Алиса может получить пустой адрес приема стандартным способом (например, SegWit V0 в Bech32).

Получив адрес приема “K0”, принадлежащий Бобу, Алиса может провести классическую транзакцию Bitcoin, выбрав на другой ветке своего HD-кошелька принадлежащий ей UTXO и потратив его на адрес “K0” Боба.

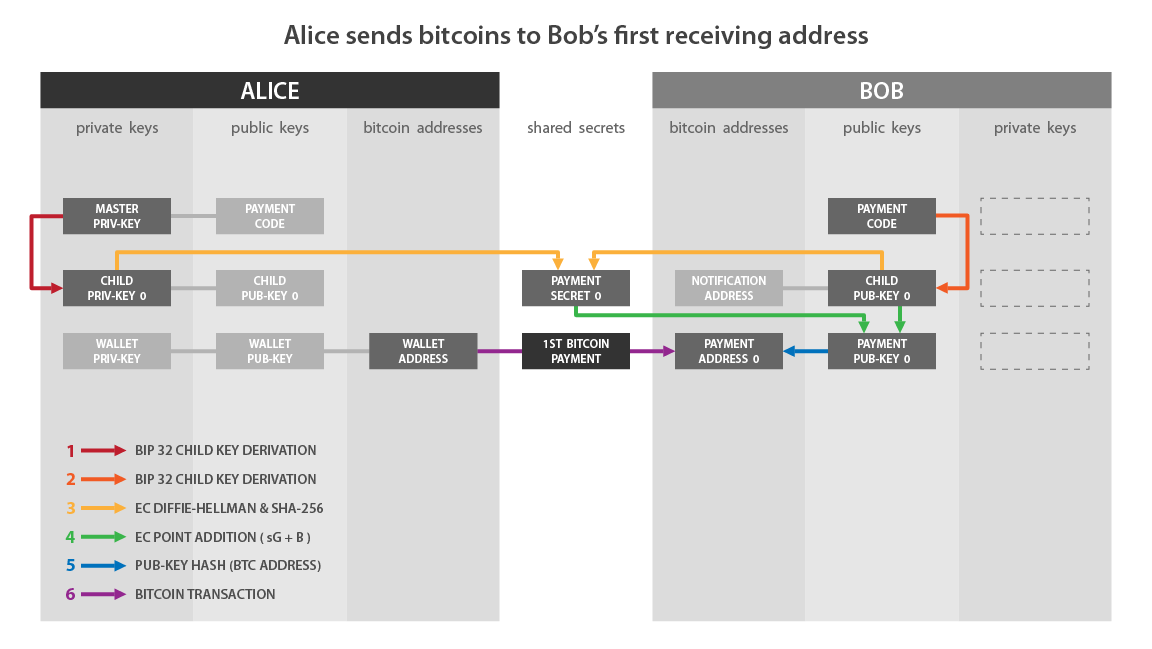
Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Если сопоставить эту схему с тем, что я описал ранее, то:

“Child Priv-Key 0” на стороне Алисы соответствует: a.
“Child Pub-Key 0” на стороне Боба соответствует: B.
“Payment Secret 0” соответствует: s.
“Payment Pub-Key 0” соответствует: K0.

Я кратко изложу шаги, которые мы только что вместе прошли для отправки платежа BIP47:

Алиса выбирает первый дочерний приватный ключ, полученный из ее персонального платежного кода.
Она вычисляет секретную точку на эллиптической кривой с помощью ECDH из первого неиспользованного дочернего публичного ключа, полученного из платежного кода Боба.
Она использует эту секретную точку для вычисления общего секрета с помощью SHA256.
Она использует этот общий секрет для вычисления новой секретной точки на эллиптической кривой.
Она добавляет эту новую секретную точку к публичному ключу Боба.
Она получает новый эфемерный публичный ключ, для которого только Боб имеет соответствующий приватный ключ.
Алиса может отправить классическую транзакцию Бобу на полученный эфемерный адрес приема.

Если она хочет произвести второй платеж, то повторяет описанные выше действия, за исключением того, что выбирает второй публичный ключ, полученный из платежного кода Боба. Другими словами, следующий неиспользованный ключ. Тогда у нее появится второй адрес приема, принадлежащий Бобу “K1”.

Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Она может продолжать в том же духе и вывести до 2^32 пустых адресов, принадлежащих Бобу.

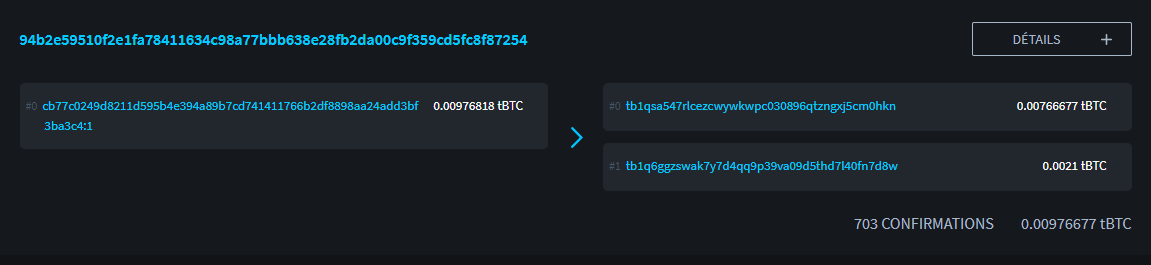
С внешней точки зрения, наблюдая за блокчейном Bitcoin, теоретически невозможно отличить платеж BIP47 от традиционного платежа. Приведем пример платежной транзакции BIP47 в сети Testnet.

TXID:

94b2e59510f2e1fa78411634c98a77bbb638e28fb2da00c9f359cd5fc8f87254

Это выглядит как классическая транзакция с одним входом, платежным выходом в 210 000 сатоши и сдачей:

Источник: https://blockstream.info/

Получение платежа BIP47 и выведение приватного ключа #

Алиса только что произвела свой первый платеж на пустой адрес BIP47, принадлежащий Бобу. Теперь давайте рассмотрим, как Боб получает этот платеж. Мы также увидим, почему Алиса не имеет доступа к приватному ключу только что сгенерированного адреса и как Бобу найти этот ключ, чтобы потратить только что полученные биткоины.

Как только Боб получает от Алисы транзакцию-уведомление, он получает публичный ключ BIP47 “K0” еще до того, как его корреспондент отправил платеж. Поэтому он наблюдает любой платеж на связанный с ним адрес. Более того, он сразу же выведет несколько адресов, которые он будет наблюдать (K0, K1, K2, K3…). Вот как он получает этот публичный ключ “K0”:

Боб выбирает первый дочерний приватный ключ, полученный из его платежного кода. Этот приватный ключ получил имя “b”. Он связан с публичным ключом “B”, с которым Алиса производила свои вычисления на предыдущем шаге:

Боб выбирает первый публичный ключ Алисы, полученный из ее платежного кода. Этот ключ называется “A”. Он связан с приватным ключом “a”, с помощью которого Алиса производила свои расчеты и который известен только Алисе. Боб может выполнить этот процесс, поскольку ему известен платежный код Алисы, который был отправлен ему вместе с транзакцией уведомления.

A = a·G

Боб вычисляет секретную точку “S” путем сложения и удвоения точек на эллиптической кривой, применяя свой приватный ключ “b” к публичному ключу Алисы “A”. Здесь мы видим использование ECDH, который гарантирует, что эта точка “S” будет одинаковой для Боба и Алисы.

S = b·A

Так же, как и Алиса, Боб выделяет абсциссу этой точки “S”. Мы назвали это значение “Sx”. Он передает это значение функции SHA256 для нахождения общего секрета “s” (строчная буква).

s = SHA256(Sx)

Точно так же, как и Алиса, Боб вычисляет точку “s·G” на эллиптической кривой. Затем он добавляет эту секретную точку к своему публичному ключу “B”. После этого он получает новую точку на эллиптической кривой, которую интерпретирует как публичный ключ “K0”:

K0 = B + s·G

Получив публичный ключ “K0”, Боб может получить соответствующий приватный ключ, чтобы потратить свои биткоины. Он единственный, кто может сгенерировать это число.

Боб берет свой дочерний приватный ключ “b”, полученный из его персонального платежного кода. Только он один может получить значение “b”. Затем он добавляет “b” к общему секрету “s”, чтобы получить k0, приватный ключ K0:

k0 = b + s

Благодаря групповому закону эллиптической кривой Боб получает именно тот приватный ключ, который соответствует публичному ключу Алисы. Таким образом, мы имеем:

K0 = k0·G

Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Если сопоставить эту схему с тем, что я описал ранее, то:

“Child Priv-Key 0” на стороне Боба соответствует: b.
“Child Pub-Key 0” на стороне Алисы соответствует: A.
“Payment Secret 0” соответствует: s.
“Payment Pub-Key 0” соответствует: K0.
“Payment Priv-Key 0” соответствует: k0.

Я обобщу только что рассмотренные нами шаги по получению платежа BIP47 и вычислению соответствующего приватного ключа:

Боб выбирает первый дочерний приватный ключ, полученный из его персонального платежного кода.
Он вычисляет секретную точку на эллиптической кривой с помощью ECDH из первого дочернего публичного ключа, полученного из кода цепочки (chain code) Алисы.
Он использует эту секретную точку для вычисления общего секрета с помощью SHA256.
Он использует этот общий секрет для вычисления новой секретной точки на эллиптической кривой.
Он добавляет эту новую секретную точку к своему личному публичному ключу.
Он получает новый эфемерный публичный ключ, на который Алиса отправит свой первый платеж.
Боб вычисляет приватный ключ, связанный с этим эфемерным публичным ключом, путем сложения своего дочернего приватного ключа, полученного из платежного кода, и общего секрета.

Поскольку Алиса не может получить “b”, приватный ключ Боба, она не может определить k0, приватный ключ, связанный с адресом приема BIP47 Боба.

Схематически вычисление общего секрета “S” можно представить следующим образом:

После того как общий секрет найден с помощью ECDH, Алиса и Боб вычисляют публичный ключ “K0” платежного адреса BIP47, а Боб также вычисляет связанный с ним приватный ключ “k0”:

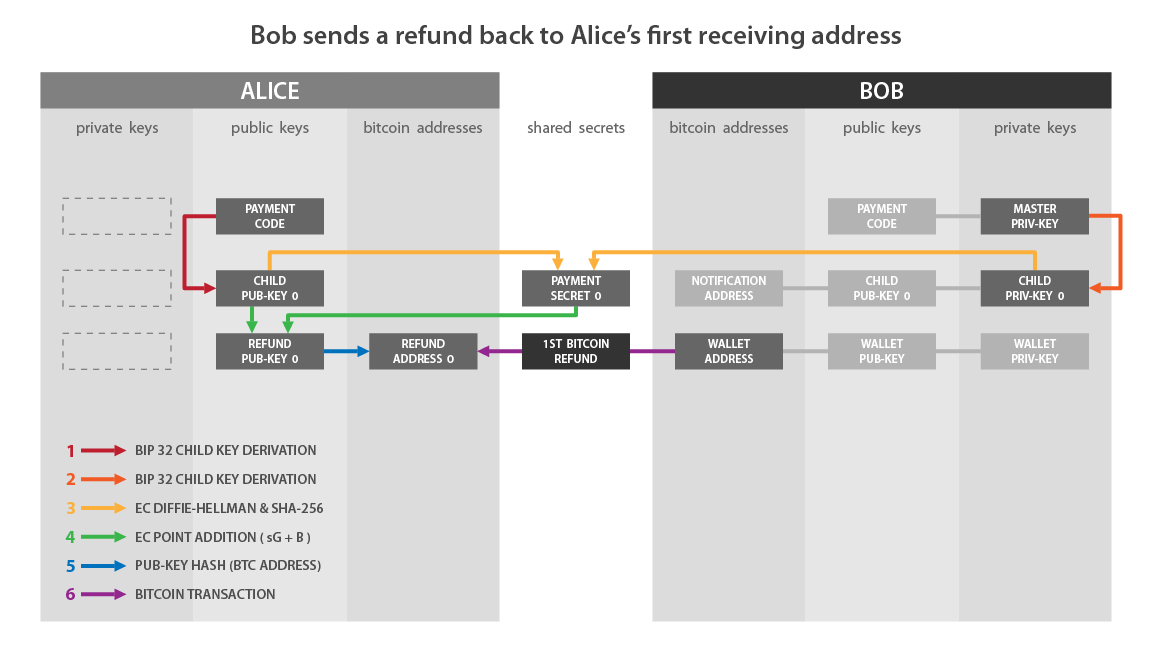
Возврат платежа BIP47 #

Поскольку Боб знает многоразовый платежный код Алисы, у него уже есть вся необходимая информация для отправки ей возмещения. Ему не нужно будет снова связываться с Алисой, чтобы запросить какую-либо информацию. Ему достаточно уведомить ее транзакцией уведомления, в частности, для того, чтобы она могла получить свои адреса BIP47 со своим сидом, а затем он также может отправить ей до 2^32 платежей.

Затем Боб может отплатить Алисе тем же способом, каким она посылала ему платежи. Роли поменялись местами:

Источник: Многоразовые платежные коды для иерархических детерминированных кошельков

Теперь вы знаете все тонкости этого великолепного решения, которым является BIP47.

Производное применение PayNym #

В результате реализации BIP47 в Samourai Wallet появились PayNym - идентификаторы, вычисляемые из платежных кодов пользователей. Сегодня их полезность выходит далеко за рамки использования BIP47.

Команда Samourai постепенно развивает целую экосистему инструментов и сервисов, основанных на PayNym пользователя. В их числе, конечно же, все инструменты проведения платежей для оптимизации конфиденциальности пользователя за счет добавления энтропии в транзакцию и, соответственно, правдоподобного отрицания.

Совместное использование Soroban, сети шифрованной связи на базе Tor, и PayNym позволило значительно оптимизировать работу пользователей при создании совместных транзакций, сохранив при этом высокий уровень безопасности. Транзакции Stowaway (PayJoin) и StonewallX2 могут быть легко осуществлены без необходимости вручную выполнять многочисленные обмены неподписанными транзакциями, необходимые для организации совместных транзакций такого типа.

В отличие от использования BIP47, поскольку для проведения этих совместных операций не требуется проведение уведомительной транзакции, для использования этих инструментов достаточно соединить (“follow”) PayNym. Подключать их не требуется.

В дополнение к этим совместным операциям мы недавно узнали, что команда Samourai работает над протоколом аутентификации, связанным с PayNym: Auth47. Этот инструмент уже реализован и может быть использован, например, для аутентификации с помощью PayNym на сайте, принимающем этот метод. В будущем, как мне кажется, помимо веб-аутентификации, Auth47 станет частью более глобального проекта, основанного на экосистеме BIP47/PayNym/Samourai. Возможно, этот протокол будет использоваться для дальнейшей оптимизации работы пользователей с кошельком Samourai, в частности, при использовании инструментов для расходования средств. Следите за новостями…

Мое личное мнение о BIP47 #

Очевидно, что основным недостатком BIP47 является транзакция уведомления. Она приводит к тому, что пользователю приходится тратить деньги на ее майнинг, что для некоторых может быть раздражающим фактором. С другой стороны, аргумент о спаме подомными транзакциями в блокчейне Биткоина абсолютно неприемлем. Любой, кто платит деньги за транзакцию, должен иметь возможность зарегистрировать ее, с какой бы целью она ни проводилась. Утверждать обратное - значит поддерживать цензуру.

Возможно, в будущем будут найдены другие, менее затратные решения для передачи платежного кода отправителя получателю, чтобы тот мог надежно его хранить. Но на данный момент транзакция уведомления остается решением с наименьшими компромиссами.

При учете всех преимуществ BIP47 этот недостаток оказывается незначительным. Из всех существующих предложений по решению проблемы повторного использования адресов, на мой взгляд, это лучшее решение.

Как было сказано выше, большая часть повторного использования адресов происходит на биржах. BIP47 - единственное разумное решение, которое действительно решает эту проблему в корне. Любое предложение по сокращению повторного использования адресов должно учитывать этот аспект и ориентировать решение на основной источник проблемы.

С точки зрения использования, несмотря на достаточно сложный механизм работы, процедура оплаты BIP47 является детской забавой. Поэтому многоразовые платежные коды могут быть легко освоены даже начинающими пользователями.

С точки зрения конфиденциальности BIP47 очень интересен. Как я уже объяснял в разделе, посвященном транзакции уведомления, платежный код не раскрывает никакой информации о полученных эфемерных адресах. Поэтому он позволяет прервать поток информации между Биткоин-транзакцией и идентификатором получателя, в отличие от традиционного использования адреса получения.

И самое главное - реализация BIP47 в виде PayNym работает! В кошельке Samourai она доступна с 2016 года, а в кошельке Sparrow - с начала этого года. Это не научный проект, а решение, которое было протестировано вчера и полностью работоспособно сегодня.

Будем надеяться, что в будущем эти многоразовые платежные коды будут приняты на вооружение игроками экосистемы, внедрены в программное обеспечение кошельков и будут использоваться биткоинерами.

Любое решение, действительно положительно влияющее на конфиденциальность пользователей, должно обсуждаться, продвигаться и защищаться, чтобы Биткоин не стал инструментом государственного надзора.

Он был чересчур счастлив, но нисколько не возгордился — доброе сердце не знает гордости, — помня то время, когда все его презирали и гнали. А теперь все говорят, что он прекраснейший между прекрасными птицами! Сирень склоняла к нему в воду свои душистые ветви, солнышко светило так славно… И вот крылья его зашумели, стройная шея выпрямилась, а из груди вырвался ликующий крик:
— Мог ли я мечтать о таком счастье, когда был еще гадким утенком!

Внешние источники и благодарности #

Спасибо LaurentMT и Théo Pantamis за множество объясненных ими концепций, которые я использовал в этой статье. Надеюсь, что мне удалось их точно передать.
Спасибо Fanis Michalakis за вычитку этого текста и экспертные советы.
https://bitcoiner.guide/paynym/
https://github.com/bitcoin/bips/blob/master/bip-0047.mediawiki
Википедия: Протокол Диффи — Хеллмана
Википедия: Протокол Диффи — Хеллмана на эллиптических кривых
https://security.stackexchange.com/questions/46802/what-is-the-difference-between-dhe-and-ecdh
https://commandlinefanatic.com/cgi-bin/showarticle.cgi?article=art060
https://ee.stanford.edu/~hellman/publications/24.pdf
https://www.researchgate.net/publication/317339928_A_study_on_diffie-hellman_key_exchange_protocols

Поддержите переводчика #

Поддержать переводчика можно, отправив немного сат в сети Лайтнинг:

lnurl1dp68gurn8ghj7ampd3kx2ar0veekzar0wd5xjtnrdakj7tnhv4kxctttdehhwm30d3h82unvwqhk7mnv093kcmm4v3unxwg6jxyqf